

Буду признателен, если поделитесь информацией
в социальных сетях
|
Я доступен по
любым средствам связи , включая видео
|
 |
 |
 |
| МЕНЮ САЙТА | |||
| Библиотека 12000 книг | ||
Видеоматериалы автора сайта
Код доступа 2461537
| Иона Охаив - Особые формы кругов на полях. |
Иона Охаив - Особые формы кругов на полях и форма локальной Вселенной
Апрель, 2004
Перевод: Любовь Подлипская
1.Введение
В 1997 и 1999 годах появились, по крайней мере, 9 кругов на полях, тесно связанных с обнаруженной формой Вселенной. То ли для того, чтобы сфокусировать наше внимание на этом скупо освещенном открытии, то ли потому, что эти геометрические формы (октаэдр и тетраэдр) видны во многих явлениях окружающей среды и на многих уровнях Природы, то ли по каким-то иным причинам, я не знаю.
2. Суперкластеры галактик в октаэдре Бетенера
Благодаря орбитальному телескопу Хаббл и другим новым телескопам вне атмосферы Земли удалось получить намного более детальные и четкие фотографии, чем сделанные с помощью телескопов, размещенных на Земле. Поэтому, начиная с 2000 года, появилась возможность сделать новую карту небес – галактик, кластеров галактик и суперкластеров галактик. Измерения радиоволн, рентгеновских лучей и так далее выявили множество невидимых галактик.
Полученные данные объединились, и оказалось, что известные супергалактики группируются вдоль линий и в точках пересечения, образуя, по крайней мере, 4 локальных определенных октаэдра, соединенных вершинами в виде кристаллического паттерна. Между и внутри октаэдров находятся относительные пустоты магнитных полей и галактик, хотя там может быть много темной материи. Это самая большая наблюдаемая структура во Вселенной.

Октаэдр, выполненный в виде оригами И. К. Герстромом
Фотография из книги Касахары и Такахамы
Это дает основания полагать, что давным-давно в истории нашей Вселенной (что также предсказывалось теорией суперструн) энергия организовывалась магнитными полями, распределялась вдоль нитей и объединялась в светящиеся группы астрономических объектов, напоминая капли воды на паутине. Темная материя сжималась и под давлением становилась светящейся.
Более того, представляется, что неясные карты космического микроволнового фона Вселенной демонстрируют сферическую форму с суперкластерами галактик в форме диска на плоском плане, напоминающего гигантский блин (гигантскую форму галактики).
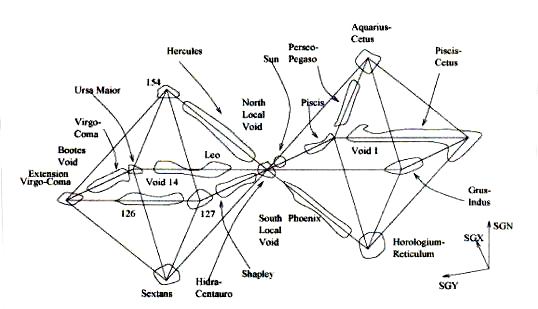
Вот два близко расположенных октаэдра, наблюдаемых с положения нашего Солнца, рядом с точкой их соединения. На вершинах и углах форм обнаруживаются суперкластеры, каждый из которых может содержать миллиарды галактик, а также пустоты. Поскольку один конец длинной области Рыбы – Кит направлен вовне, можно вытянуть даже более крупномасштабную форму.
Судя по незначительному положению в нашей Галактике, Млечный Путь, наше Солнце вряд ли является главным центром Вселенной. Поэтому, мне интересно, можно ли увидеть октаэдры на обеих сторонах от почти любого занятого положения в пространстве?
Вот плоская карта четырех октаэдров (и частично еще двух), которых мы можем реально наблюдать в небе, потому что они находятся в ближайшей к нам области пространства.
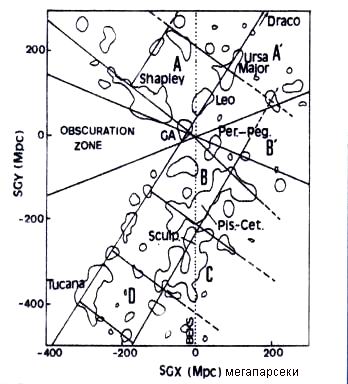
(mpc – мегапрасеки)
(сверху вниз: Дракон, Большая Медведица, Шеплиевский, Лев, Зона Потемнения, Персей-Пегас, Рыбы-Кит, Ваятель, Тукана)
А вот та же область с трехмерными октаэдрами. “А” и “В” – самые близкие к нам формы. “С” и “D” находятся от нас дальше, поэтому они наблюдаются и оцениваются менее точно.
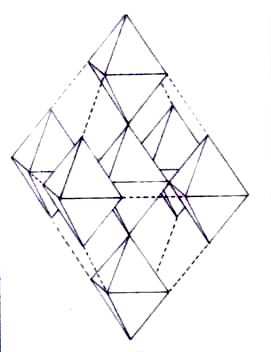
Каждый октаэдр может фрактально содержать под-октаэдры. Выше и ниже приведенные рисунки демонстрируют самую простую возможность: 7 под-октаэдров, объемом в одну треть большей формы. Следующей самой простой формой было бы 25 под-октаэдров, объемом в одну пятую большего октаэдра.

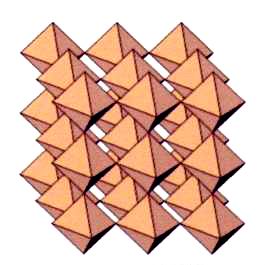
Согласно ныне господствующей теории, наблюдаемые астрономические октаэдральные формы могут иметь только один меньший фрактальный масштаб или повторение перед тем, как исторические силы радиации будут сбрасывать необходимый магнетизм, разрывая меньшие вершины/нити в пространстве. Однако в пространстве вполне возможно любое число больших повторений, то есть октаэдров в больших октаэдрах и так далее.
Согласно теории “яичного лотка”, возможно любое число соединенных вершинами октаэдров.
3. Трехмерные примеры на уровне Солнечной системы
Наше Солнце тоже обладает системой магнитного поля в форме октаэдра: северный полюс, южный полюс и 4 полюса вдоль экватора. Все эти точки Солнца испускают потоки заряженных энергетических частиц.
Рисунок Дэвида Уилкока
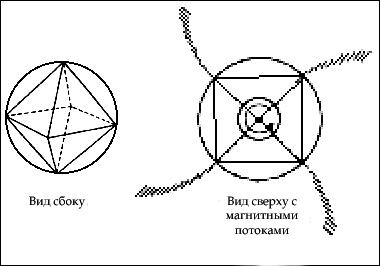
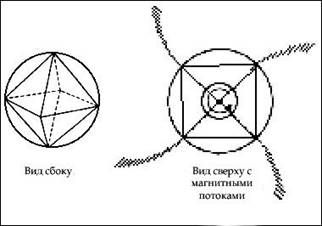
С другой стороны, когда в сферической планете размещается звездный тетраэдр, точки пересечения сферы и тетраэдра или геометрические “точки напряжения”, находящиеся на широте 19,47º, часто демонстрируют высвобождение огромных энергий и взаимодействие подпочвы планеты с атмосферой. Очевидно, непрерывные вибрации планеты создают здесь меньшее давление, куда устремляется более высокое давление. Примерами могут служить постоянные бури Огромного Красного Пятна на Юпитере, Огромное Темное Пятно на Нептуне, вулканическая область Гавайев на Земле, самые большие “солнечные пятна” или высоко энергетические испускания Солнца.
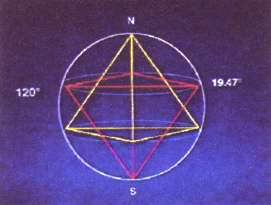
Само Солнце (ближайшее к стрелке-указателю) спиралевидно вращается вокруг рукава Млечного Пути. В свою очередь, четыре спиралевидные орбиты – это четыре ближайшие к Солнцу планеты: Меркурий, Венера, Земля и Марс.
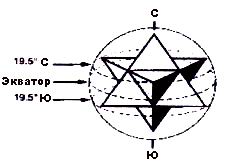
На верхнем рисунке показаны пропорции среднего орбитального расстояния от Солнца Меркурия и Венеры. На нижнем рисунке показано, что орбита Меркурия будет проходить через центры трех смежных окружностей, а Венера движется по касательной к этим трем окружностям.
4. Платоновы твердые Тела

Все Платоновы Твердые Тела совершенно вписываются в сферу, и многие из них могут совершенно вписываться в большие версии друг друга.
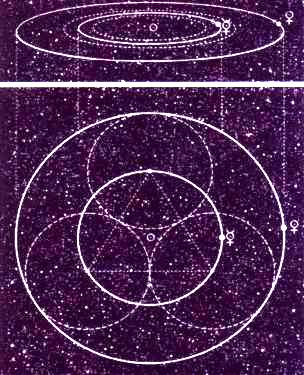

Вышеприведенные иллюстрации заимствованы из книги Джона Мартино “Маленькая книга совпадений”.
Кеплер выдвинул гипотезу, что орбитальные расстояния шести ближайших планет от Солнца могут содержать между собой формы пяти Платоновых Твердых Тел. Разновидности эллиптических орбит планет содержались бы в толще разделяющих их сферических оболочек.
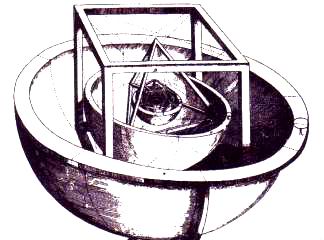
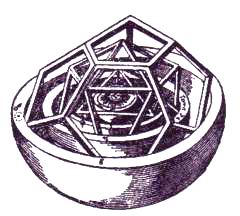
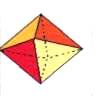
Октаэдр – это симметричное твердое тело, обладающее поверхностью в виде 8-ми равносторонних треугольников. То есть, это две четырехгранные пирамиды, соединенные своими основаниями. Фигура в центре – октаэдр с квадратом в середине.
Оригами тетраэдра, сделанное И. К. Герстромом
из книги Касахары и Такахамы

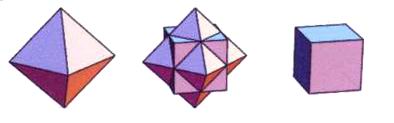
Иллюстрация из статьи «Углубленное изучение»
Тетраэдр – это симметричное твердое тело, обладающее поверхностью в виде четырех равносторонних треугольников. Он похож на пирамиду с тремя сторонами и основанием. Это самая простая трехмерная симметричная форма с прямыми линиями, как треугольник – самая простая двумерная форма.
Вышеприведенные рисунки показывают три вида тетраэдра. Первый, с пунктирной линией, показывает наклонный вид сбоку. Второй зависит от того, как вы фокусируете центральную точку – вид сверху, рассматривание нижней поверхности и двух сторон или рассматривание прозрачно через переднюю поверхность. Третий – это рассматривание либо задней поверхности, либо через вершину двух прозрачных сторон. Заметьте, если смотреть сверху, то виден также октаэдр!

Тетраэдр – это единственный правильный многогранник (трехмерная форма с равными сторонами и углами на всех поверхностях), который повторяется на меньших планах. Соединяя точки на серединах сторон, в его внутреннем пространстве можно получить меньший тетраэдр, и так далее и так далее.

Если смотреть на одну из его сторон, тетраэдр выглядит как равносторонний треугольник, в свою очередь содержащий четыре меньших равносторонних треугольника.
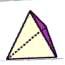
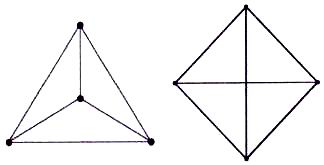
Если смотреть сбоку, тот же тетраэдр в той же сфере дает треугольник внутри круга. Верхние углы находятся на ранее упомянутых 19,5º над “экватором” сферы.
Отношения в обеих иллюстрациях часто обнаруживаются в паттернах кругов на полях, содержащих треугольники.
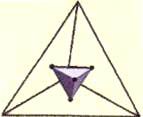
Иллюстрация Берта Дженсена
Два тетраэдра могут быть вставлены друг в друга, и образовывать “звездный тетраэдр”, двумерное изображение которого дает “Звезду Давида” или “Печать Соломона” (отца Давида), известную своими тонкими, эзотерическими уровнями значений.
Наряду с другими способами, его можно рассматривать как связанную систему, либо в состоянии покоя, либо движущуюся в одном направлении. Или, например, когда зеленый тетраэдр вращается по часовой стрелке, а красный – против часовой стрелки. Или как перпендикуляры, где зеленый вращается горизонтально, а красный – вертикально.
Насколько я понимаю ссылки Йена Роуолда на Ричарда Хоагленда и физику тетраэдра Стэна Тенета, путь энергии, идущей из центра вращающейся сферы к ее поверхности, будет спиралевидным, создавая тетраэдр, касающийся поверхности сферы. Перпендикулярно вращающиеся тетраэдры будут генерировать спиралевидную энергию, создающую электромагнитные линии, вдоль которых энергия будет собираться в материю. Вращающиеся тетраэдры разных размеров будут сцепляться.
Говорят, что энергия из более высоких, вращающихся, более мощных планов спиралевидно закручивается внутрь и вниз к нашей атмосфере (образуя форму перевернутой вращающейся пирамиды), пока не сфокусируется в точке. Затем она спиралевидно закручивается вовне (как пирамида, вращающаяся в противоположном направлении) к земле. Например, пирамиды Египта являются устройствами, фокусирующими энергию между Землей и внешним Космосом.
Они связывают атмосферу с землей как растущая структура распределения листьев дерева или веток по сравнению с корневой системой. Свежая энергия спиралевидно входит в пульсирующие, потребляющие, живые организмы, из которых выходит спирали уже переработанной энергии. Стекая в ванне или раковине, вода тоже движется по суживающимся спиралям.
5. Фрактальный тетраэдр Чилболтона
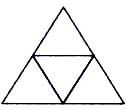
Такая форма или расположение компонентов позже использовалась в технологии сотовых телефонов. Геометрически этот круг на полях закономерно увязывается со ставшим известным позднее “Лицом” Чилболтона и кругами на полях “Код инопланетян” (“код”, детально описывающий инопланетное существо).
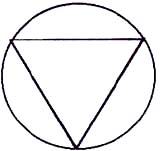
Иллюстрация Ника Коллестрома
Фрактал Серпинского
Расширяя фрактал, мы получаем треугольник, сделанный из меньших треугольников, или, если смотреть сверху, пирамиду, сделанную из постепенно уменьшающихся уровней меньших пирамид.
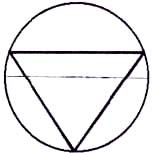
Иллюстрация Берта Дженсена
Как мы вскоре увидим, красные треугольники внутри зеленых могут так же представлять вид сбоку трехмерных, меньших октаэдров, встроенных в тетраэдр.
Как еще соотносятся октаэдр и тетраэдр? Если вы разместите два октаэдра один позади другого с общей вершиной, пространство между ними будет заполнено тетраэдром. Поэтому если вы возьмете один большой октаэдр и заполните его меньшими октаэдрами с соприкасающимися вершинами, все пространство между ними будет заполнено тетраэдрами.
6. Трехмерный октаэдр Овертона
Фотография Стива Александера
Западный Овертон, 24 июня 1999 года
Меньшие формы круга на полях напоминают шестиугольники, а не окружности.

Октаэдр
6 вершин, 12 ребер, 8 граней
Иллюстрация Майкла Гликмана/Патриции Мюррей
Трудность демонстрации вращающихся твердых тел в символах кругов на полях состоит в том, чтобы изобразить в двух измерениях четыре (или более) измерений.
Беря из этого круга на полях только пути (убирая маленькие шестиугольники и рассматривая большие шестиугольники как точки на линиях) и сворачивая по линиям, мы получаем трехмерный октаэдр.
Заметьте, что двумерное изображение октаэдра слева дает квадрат, а справа – шестиугольник, помимо треугольной формы, на которой мы фокусировались раньше.

Добавляя меньший тетраэдр к каждой стороне октаэдра, мы получаем звездный тетраэдр.
Сейчас заметьте, что круг на полях снизу слева, свернутый в октаэдр, вмещает большие и меньшие шестиугольники как укрепляющие паттерны вдоль ребер и вершин.
Более того (как красиво нарисовано), заметьте, что октаэдр увязывается с областью пересечения звездного тетраэдра. Возможно, на каком-то уровне огромный, вновь открытый октаэдр Вселенной окажется внутри либо звездного тетраэдра, либо других симметричных форм Платоновых Тел.
7. Пирамидальные фракталы Уиндмил Хилл и Западного Кеннета
| Аудиокниги | Музыка | онлайн- видео | Партнерская программа |
| Фильмы | Программы | Ресурсы сайта | Контактные данные |
|
Этот день у Вас будет самым удачным! Добра, любви и позитива Вам и Вашим близким!
Грек
|

|
каталог |