ФРАНКЛИН МЕРРЕЛЛ-ВОЛЬФ

МАТЕМАТИКА, ФИЛОСОФИЯ И ЙОГА

Перевод К. Семенов Редактор В.Трилис

Пер. с англ. — К.: «София», Ltd., 1999. —160 стр. ISBN 5-220-00211-2  ©«София»,1999

«Математика, философия и йога» — самый памятный из многочисленных курсов лекций, прочитанных Франклином Меррелл-Вольфом за многие годы. Эти лекции выде­ляются не только своей исключительной содержатель­ностью, но и глубиной воздействия на слушателей.

То, о чем говорил Вольф, захватывает, бросает вызов интеллекту. Его сверхзадача, несомненно, заключалась в том, чтобы вызвать у присутствующих некое сверхъестест­венное состояние, дать им прямое осознание того невыра­зимого, что было источником его слов.

ПРЕДИСЛОВИЕ РЕДАКТОРА АМЕРИКАНСКОГО ИЗДАНИЯ

«Математика, философия и йога» — самый памятный из многочисленных курсов лекций, прочитанных Франкли­ном Меррелл-Вольфом за многие годы. Эти лекции выде­ляются не только своей исключительной содержатель­ностью, но и глубиной воздействия на слушателей. На пер­вый взгляд может показаться, что три указанные в наз­вании темы настолько различны, что их невозможно сов­местить в рамках одного курса лекций. Однако йога («еди­нение» с высшей Действительностью) является существен­но практической дисциплиной, цель которой —привести к Просветлению; сходным образом, Вольф считает филосо­фию — в ее изначальном смысле «любви к мудрости» — Путем Осознания [I] (Пробуждения к Трансцендентному [2]Сознанию). Кроме того, следуя духу Пифагора, он при­бегает в собственном поиске к созерцанию и к математи­ческим понятиям, пользуясь ими не только для такого пре­ображения сознания, но и для доступного пониманию опи­сания подобных состояний. Все это дает Вольфу основания считать себя первопроходцем «математической йоги» — дисциплины естественной и уместной в западной культуре. В его изложении, таким образом, объединились три пред­мета, каждый из которых отражает свои аспекты единой проблемы — духовного поиска.

Эти лекции были записаны на магнитофонную ленту, но последующий перевод в письменную форму и редактирование оказались несколько затруднительными: матема­тические схемы и иллюстрации пришлось восстанавливать по неполным словесным описаниям, а соответствующие фрагменты текста видоизменить во избежание очевидных для читателя указаний («здесь», «вот это» и т. п.). Намного важнее — и труднее — было передать живость личного общения; поэтому я позволял себе лишь минимальные поправки и изменения, сохраняя первоначальную непри­нужденность беседы. С той же целью сохранены попутные замечания автора, но ссылки и редакторские ремарки отне­сены в конец книги.

То, о чем говорил Вольф, захватывает, бросает вызов интеллекту; однако живая связь с аудиторией во время лекции была еще важнее и сильнее, чем формальное изло­жение. Его сверхзадача, несомненно, заключалась в том, чтобы вызвать у присутствующих некое сверхъестествен­ное состояние, дать им прямое осознание того невыразимо­го, что было источником его слов. В результате оказалось, что метод изложения не менее могуществен, чем познава­тельное содержание сказанного. Тембр голоса, интонации, подбор слов, фразировка и многие другие тонкие инстру­менты как раз и служат созданию такой атмосферы. Поэто­му я как редактор заботился прежде всего о том, чтобы сохранить особенности стиля Меррелл-Вольфа, создать ощущение его личного присутствия и попытаться вызвать у читателя тот эмоциональный отклик, который благопри­ятствует зарождению чувства Трансцендентного.

Рон Леонард

ВВЕДЕНИЕ

Я прослушала курс лекций «Математика, философия и йога», прочитанный в 1966 году. В то время я была юной мамой четырех маленьких детей, а также внучкой лектора, Франклина Меррелл-Вольфа. Все шесть лекций читались в гостинице «Лос-Оливос», рядом с публичной библиотекой «Феникс» в самом центре города. Стоял ноябрь — особенно приятное время года на юге Аризоны, тот период, когда люди только начинают выходить из летней летаргии. Количество слушателей, среди которых было примерно поровну мужчин и женщин, колебалось в преде­лах от тридцати до шестидесяти человек.

Каждый вечер я упорно пыталась понять, о чем идет речь. Однако, одновременно с расширением сознания че­рез мышление, Франклин пользовался тем, что называл «Потоком». Мое восприятие Потока представляло собой постепенно углубляющееся осознание полной телесной расслабленности. Видимые образы становились расплывчатыми и обширными. И одновременно появлялось ощуще­ние глубокого мира и тишины. Безмолвие успокаивало ра­зум и чувства. Благодаря этому покою я понимала его рас­сказы о математическом и философском подходе к йоге. Упорная борьба за понимание прекратилась, но само пони­мание все равно случалось. Успокоив эмоции, я стала нам­ного глубже погружаться в пространство сердца, и это при­носило радостную усладу. Я поняла, что эмоциональный покой углубляет любовь до уровня более безусловного чувства сострадания.

Мне вспоминается вечер 18 ноября, дня моего рождения. После лекции я стояла посреди гостиной своего дома, а рядом были Франклин и Гертруда (его вторая жена), Уэс (мой муж) и мои родители (Джим и Хелен Бриггз). Я была исполнена блаженства! Я ощущала такое счастье, что его трудно было удержать в себе... Мне хотелось танцевать, издавать ликующие возгласы и бурно благодарить всех за то, чему я по-прежнему не могла найти подходящего опи­сания. Я поделилась этими чувствами с Франклином. Он улыбнулся той знающей улыбкой, от которой у его глаз всегда собирались морщинки, и сказал: «Да, да. Сегодня вечером ты побывала в Потоке».

Дороти Леонард

Лекция 1

С 1936 года я поднимаюсь на эту кафедру с одной и только одной целью: хоть немного доступнее передать смысл того, что называют Осознанием. Этому есть основа­ния, и они связаны с проблемой человечности. Взгляд, бро­шенный на человеческую историю в том виде, в каком она нам известна, отмечает прежде всего одну ее яркую особен­ность: это —летопись бесчеловечного отношения человека к человеку. Будда сказал, что величайшим уделом скован­ного двойственным сознанием человечества было страда­ние, проявляющееся в непрерывных войнах, порабощени­ях и эксплуатации. Трагическое содержание мы видим не только в исторических хрониках, но и в частных пробле­мах, с которыми сталкивается каждый человек. Существует проблема смерти — ведь ко всем нам обращено ее отврати­тельное обличье. Нет сомнений, это далеко не все, но это то, что мы видим. Существует проблема осмысления того бес­конечного круга, который, на первый взгляд, совершает свои обороты без какого-либо развития и движения впе­ред. Я мог бы продолжать, но все это — часть двойственно­го сознания, известный нам обыденный мир, где попытки человека воспользоваться средствами такого сознания с тем, чтобы избавиться от страданий — задача нерешенная и, видимо, неразрешимая, — никогда не приводили к ус­пешному результату. Я не буду останавливаться на этом подробнее; думаю, одного лишь упоминания достаточно, чтобы вы вспомнили об этих фактах.

Двойственное сознание раздвоено по меньшей мере по трем причинам. Важнейшей из них являются взаимоотно­шения между объектом и субъектом. Эта мысль уже стала привычной. Мы познаем нечто только путем сравнения с его противоположностью. Высшее понятно нам только в сравнении с низшим, добро — при противопоставлении злу, и это относится ко всем парам противоположностей. Без сопоставлений мы не познали бы ничего. Сознание двойственно и по той причине, что обладает только двумя функциями, органами или способностями познания, а именно чувственным восприятием и умозрительным пос­тижением.

Действительно, были такие, кто достиг освобождения. Правда и то, что есть способ достичь его, что существует горстка людей, не оставивших человечество в одиночестве. Я мог бы упомянуть Кришну, Будду, Христа, Шанкару, Лао-цзы, Аполлония Тианского, Мейсгера Экхарта, Якова Бёме и многих других, известных и забытых. Не будь их, челове­чество уже давно кануло бы в вечность. И все же единицы среди миллиардов — это не так уж поразительно. Да, я понимаю, некоторые возразят, что сейчас обстоятельства изменились. Мы добились изумительных достижений в ак­сиоматических науках — они действительно впечатляют. Многие из свершений просто невообразимы, но именно из-за этой науки все мы, живущие в нашем мире, сидим на пороховой бочке. Мне приходится признать, что этот от­рицательный факт сводит на нет всю положительную цен­ность аксиоматических наук. Сегодня военные говорят о нашей стране на языке минимальных и максимальных воз­можных потерь, которые могут составить от семидесяти до ста тридцати миллионов. Была ли в истории эпоха столь опасная, исполненная такой мрачной угрозы? Вероятно, мы можем считать аксиоматические науки некими демони­ческими силами, уничтожающими больше, чем они созда­ют! Дверью к разрешению проблемы человеческих страда­ний, этого вопроса, остающегося без ответа, является то, что мы называем Осознанием.

Сегодня я попробую внести некоторую ясность в ту систему понятий, которая нам необходима. Сначала начер­тим горизонтальную прямую (см. рис. 1).

  НЕДВОЙСТВЕННОЕ СОЗНАНИЕ (непрерывное пространство) 

ДВОЙСТВЕННОЕ СОЗНАНИЕ (дискретное пространство)

Рис.1

Ниже прямой простирается область двойственного сознания, а выше — область недвойственности, куда разум не способен проникнуть без помощи со стороны. Я утверж­даю, что разум в состоянии самостоятельно превзойти лю­бую ранее достигнутую высоту и что и в дальнейшем он никогда не достигнет уровня, который не смог бы затем перерасти. Но выше этой линии ему все же не подняться. Те из вас, кто знаком только с примитивной логикой детского сада, могут заявить, что я противоречу себе. Ничего подоб­ного. Думаю, слушатели с математическими познаниями уже предвидят ответ. Считайте эту линию пределом в том смысле, в каком это понятие используется в дифференциальном исчислении. Чтобы проиллюстрировать принцип предела, рассмотрим такой ряд:

1 + 1/2 + 1/4 + 1/8 + ... + 1/n + ...

Начертим отрезок и изобразим эту сумму геометричес­ки (см. рис. 2).

|----------------|--------|----|--|-|||

Рис.2

Обозначим его левую границу числом 0, середину — 1, а противоположный конец — 2. Процесс суммирования членов ряда можно представить последовательностью то­чек. Прибавление каждого последующего члена делит ос­тавшуюся часть отрезка пополам. После бесконечного (и никак не меньше!) числа шагов сумма ряда станет равна двум, однако этого значения невозможно достичь никаким конечным количеством сложений. Двойку нельзя полу­чить, даже если складывать эти уменьшающиеся дроби на протяжении целого гугола лет. Гугол представляет собой вот такое число:

₁₀100

Это название придумали ребята из одного детского са­да, когда им изложили идею огромных чисел, — как ни странно, дети смогли ее воспринять [1]. Помимо прочего, это указывает на то, что мы рождаемся с дремлющими представлениями обо всей совокупности как известной ма­тематики, так и любой математики, какая только может возникнуть в будущем. Я мог бы обсудить некоторые тео­ретические недостатки этого утверждения, но пока давайте считать это просто неким положением. Чтобы получить представление о продолжительности гугола лет, достаточно сказать, что в сравнении с ним сотня лет Брахмы [2] выгля­дит краткой передышкой.

Именно в таком смысле необходимо понимать и мои слова о том, что разум не в состоянии подняться выше начерченной линии на рис. 1, хотя может превзойти любой уровень, которого уже достиг или достигнет в будущем. Это означает, что, имея в своем распоряжении конечное время, вы всегда способны совершить еще одну операцию сложения. Иными словами, разум может возвыситься до такой степени, что его удаленность от этой прямой окажет­ся меньше любого предопределенного расстояния, каким бы малым оно ни было. Можно возразить, что такие подъ­емы будут несущественными, так как изменения расстоя­ний слишком малы, но это не совсем так. Подобные свер­шения могут оказаться очень значительными — я здесь не ставлю никаких ограничений. Таким образом, без посто­ронней помощи разум может вечно двигаться ввысь — но он никогда не пересечет этой прямой. То есть навсегда ос­танется в области двойственного сознания.

В этом курсе лекций меня больше всего интересуют способности, присущие разуму, то есть свойства умозри­тельного постижения. Совершенно понятно, что это не единственное качество, обеспечивающее движение вперед, но в рамках данного курса лекций нам предстоит уделить основное внимание именно умозрительному познанию и тому, как использовать его для Осознания. Под Осознанием мы будем понимать любое, пусть даже не очень глубокое проникновение в недвойственность.

Видимо, сейчас мне придется сделать достаточно длин­ное отступление, так как пока что я просто начертил ли­нию, границу между чем-то высшим и низшим. Это не полная картина, вот и давайте набросаем более полную.

В автобиографии Карл Юнг [3] сравнивает человека в сфере двойственного сознания с неким ящиком, подвешен­ным на нити. Юнг практически покинул этот ящик, когда был на грани смерти; он по собственной воле вернулся на­зад, хотя и сожалел о том, что вновь оказался на той точке зрения, с которой заключенное в ящик сознание считается нормальным. Я не помню, говорил ли он, что у этого ящика есть окна или же он лишен окон, подобно монадам Лейбни­ца [4]. Я невольно вообразил себе нечто вроде овальной клетки—эллипсоида, вращающегося трехмерного эллипса (см. рис. 3).

Человек здесь двигается в ограниченном пространстве на некотором расстоянии от всего прочего — одиночество в самом подлинном смысле этого слова: ни вообразить, ни поверить невозможно. Этот образ можно отнести как к личности, так и ко всему человечеству. Вокруг человека, заключенного в такой овал, тянется обширное пространс­тво; оно простирается не только выше, но и ниже, со всех сторон. В аналитической психологии все это — и вверху, и внизу, и справа, и слева, и впереди, и сзади — называют Бессознательным. Крошечная зона сознания в этой обо­лочке и представляет собой весь известный нам обычный мир. Конечно, сквозь оболочку часто проникают некие воз­действия, источник которых не удается отследить, однако не все они возвышенны. Одни — мрачные, другие — нейт­ральные, третьи — соблазнительные, увлекающие в ловуш­ки. Недостаточно просто выйти, разрушив стенку оболоч­ки; неизмеримо важнее — как именно это произойдет. В наши дни царит увлечение определенными химическими веществами, обеспечивающими прорыв наружу, но они требуют осторожности! Причиненный ущерб едва ли удас­тся исправить даже на протяжении всей жизни. Более того, я считаю любые практики тантрического толка подозри­тельными и сомнительными для западного человека. И я бы не рекомендовал пранаяму, асаны, мудры, мантры или средства подъема кундалини как совершенно безопасные упражнения [5]. Вполне возможно, что где-то — вероятнее всего, на Востоке — найдутся люди, которые могут без рис­ка, под руководством опытного гуру пользоваться подоб­ными методами как средствами, но вообще этот путь чре­ват потенциальным вредом. Помните, мы стремимся к воcхождению сознания, а не просто к выходу из клетки двойс­твенного сознания в произвольном направлении. В выши­не небесное, внизу адское—вот в чем опасность. Есть лишь один безопасный путь, и он требует, чтобы ищущий пожер­твовал всем, чем владеет, отбросил все, чем является, перес­тал цепляться за пустоту — за богатство, общественное положение, должность, семью, излюбленные представле­ния и саму жизнь. Только такой путь надежен. Важно лишь это. Все прочее, включая приемы медитации, относится к средствам и не является существенным.

Конечно, может возникнуть вопрос: «Что останется, если я пожертвую всем?» Слово «жертвовать» означает «освящать»*. Кроме того, это, разумеется, передача чего-то Иному, высшему Иному — тому, что проявляется как Ну-мен**. Я намеренно пользуюсь научным понятием. Я пыта­юсь избежать религиозной терминологии, так как дух вре­мени заставляет нас, людей Запада, больше прислушивать­ся к науке, чем к обычной религиозности. Я вполне мог бы говорить на языке религии, но предпочитаю термины, свя­занные с духом времени. Научное название божественнос­ти: «Numen», а соответствующее прилагательное: «numino­us»***. Нумен — факт действительности, его можно ощу­тить. Я знаю это! Это не теория! Жертва предназначена Нумену. Вообще говоря, то, что укладывается на жертвенник, возвращается очищенным; с другой стороны, хотя прежде жертва казалась личной собственностью человека, она вновь вручается ему как попечителю, управляющему, которому предстоит распоряжаться подобными жертвами — благосостоянием, проницательным разумом, взаимоот­ношениями, самой жизнью — во благо великого Целого, Всего Сущего. Быть может, возвращается далеко не все, но если так, то это еще правильнее.

Итак, для следования Пути важно полное опустошение без попыток сберечь какую-либо часть, сохранить особые предпочтения. Люди временами обманывают самих себя и скрывают собственные привязанности, называя их испол­нением долга: «У меня есть определенные обязательства перед этими людьми. Заботиться о них — мой долг. Я не могу принести его в жертву». В действительности это озна­чает, что человек не доверяет Нумену, Высшей Силе. Все эти внешне благородные объяснения — лишь маскировка привязанности. Существует нравственная дисциплина. Что касается прорыва в Трансцендентное, то основным его принципом служит чистота —не только в достаточно при­вычном нам значении избегания откровенно отвратитель­ных мыслей, но и в ином, более исчерпывающем смысле полной самоотдачи. Это та чистота, которая означает нес­мешанные побуждения, незапутанное мышление. Одним из величайших уроков чистоты является изучение чистой математики.

Вот что по-настоящему важно, и с течением времени, в один прекрасный день — ведь существует закон циклов, неизбежно приближающий назначенный час, — линия над головой разрывается, распахивается. Вы можете слышать слова или получать знания в полном безмолвии. «Перед тобой раскрываются все богатства Беспредельности. Бери все, что сможешь взять!» Глуп тот, кто ответит: «Мне дос­таточно и одной жемчужины». Не жалея сил, погружайтесь в Глубины, которые одновременно являются и Высотами. Это Путь Мудрости, но вам потребуется большая смелость. Я могу сказать, что на этом пути есть особые остановки. На одной из них — далекой, хотя и не последней — можно ощутить, как тебя охватывает Нумен, избавляющий от лю­бого бремени, одаряющий завершенностью успокоения, окутывающий блаженством, которое выходит за рамки постижимого. Это реально. Я пережил его, это ощущение небесной сладости, но оно по-прежнему двойственно и не является окончанием пути. В этом заключается цель бхакти [6], но это еще не Отождествление; тот, кто зашел так дале­ко, уже в безопасности, но рискует надолго задержаться. Великая, хотя, быть может, и не такая сладостная цель Осоз­нания Тождественности находится еще дальше. Она озна­чает отождествление с Парабрахманом [7] — не с крошеч­ной крупицей Парабрахмана, но, как указывает Шанкара [8], со всей его полнотой. Это требует смелости. И хотя это тоже не последняя ступень восхождения, но уже родные края.

Многие из вас могут непонимающе возразить: «Это не более чем безмерная гордыня, напыщенность — психоло­гическое проявление чудовищно разросшегося эго». Знае­те, есть история про одного чела [9], который пришел к несколько несовершенному осознанию тождественности Парабрахману. Он шел со своим гуру по лесной тропе, а навстречу двигался слон с погонщиком на спине. Погоншик крикнул: «Посторонитесь, дайте слону пройти». Но чела не свернул с пути, и слону пришлось охватить его хоботом, чтобы перенести в сторонку. Чела был потрясен! «Как слон мог так поступить? Ведь я — Парабрахман!» Гуру ответил: «Ты не послушался Парабрахмана, обращающего­ся к тебе устами погонщика, и потому Парабрахман-ел он перенес тебя в сторону». Чела сделал большую ошибку: осознал «Я есть ТО», но забыл добавить «...и ты тоже». Вот в чем разница между напыщенностью и настоящим отож­дествлением.

Я надеюсь, что позже, когда мы перейдем на более строгую математическую почву, мне удастся путем логичес­ких аналогий с математикой бесконечных величин пока­зать вам, как личность и в то же время все прочие существа могут стать тождественными всей полноте Парабрахмана. Это действительно так, просто мы позабыли всеобщую ис­тину. На самом деле, мы не становимся ТЕМ. Мы пробуж­даемся, вспоминаем забытый, но вечно истинный факт. На языке буддистов, которые пользуются иной терминологи­ей, это выражается утверждением о том, что каждый чело­век (и не только человек, а любое существо) — уже Будда, он просто забыл об этом и страдает из-за своего неведения. Единственная разница между обычным человеком и дос­тигшим Осознания заключается в том, что последнему из­вестна эта истина. Однако он не создает нового факта: этот факт справедлив для всех.

Сейчас я делаю краткие наброски того, что станет веду­щей темой наших дальнейших бесед. Сегодня я не предла­гаю определений, они появятся позже. Я пока не забочусь о тех подробностях, которые займут надлежащее им место в последующем изложении. В отношении разума я скажу, что это, вероятно, величайшая (во всяком случае, потенци­ально самая могущественная) сила адхары, двойственного сознания; но, несмотря на это, мне придется четко опреде­лить, на что она не способна. Я говорю о самостоятельном разуме, то есть разуме, действующем исключительно свои­ми силами. Тот разум, который научился приносить жерт­вы и подчинять себя иной силе, в состоянии подняться в высшие области. Если же он не покоряется, если остается орудием гордыни, то может привести своего хозяина к асурическим [10] искушениям. Такое возможно, и я это знаю. Я подумал, что определенную ценность для вас может представлять различение двух типов сознания — того, что находится выше черты, и того, что простирается ниже, — в той мере, в какой я знаком с ними и способен выразить эту разницу словами. Прежде всего, сознание, которое называ­ют «двойственным», можно именовать «дискретным», так как оно проявляется в категориях многообразий. Вероятно, эти термины более доступны математикам, чем прочим людям. В качестве примера многообразия я могу предло­жить ряд обычных натуральных чисел: 1, 2, 3, 4 и так далее, до бесконечности. Одно число расположено рядом с дру­гим, тройка следует за двойкой и стоит перед четверкой. Рассматривая набор, или совокупность, такого рода, вы мо­жете назвать его «многообразием», или «дискретным прос­транством», поскольку, подобно песчинкам, каждый эле­мент этого множества отделен от остальных и рядом с лю­бым из них найдется определенный соседний элемент. В противоположность этому, существуют множества, для ко­торых это правило не выполняется; они называются «непрерывными». В качестве примера я возьму не только целые числа, но и все дроби, то есть величины в форме а/b, где a и b — целые (b не равно 0). Добавим также числа вида “Va” (корень n-ой степени из а), которые иногда сводятся к це­лым числам или к сочетанию целого числа и дроби, но чаще всего оказываются так называемыми иррациональными величинами. Примером может служить V2 — это число невозможно привести в полной форме: 1,41421..., так как для его точной записи потребуется бесконечная последова­тельность цифр. Класс подобных чисел называют «ирраци­ональными» [11]. Можно утверждать, что V2 больше, чем 1,41421, но меньше, чем 1,41422. Можно ограничить это число интервалом любой длины, но нам никогда не найти его точного выражения. Даже если записать ряд чисел, со­держащий в себе все дроби и указанные иррациональные величины, количество оставшихся неучтенными чисел по-прежнему будет бесконечным. Таково характерное свойс­тво непрерывного пространства, или континуума. Прин­цип непрерывности чрезвычайно важен для дифференци­ального исчисления.

Используем концепцию непрерывности как аналогию того сознания, которое расположено выше черты (рис. 1). Здесь нет ничего отдельного, дискретного. Все, можно ска­зать, пребывает в текучем состоянии. Это свойство тесно связано с анализом движения, где не существует дискрет­ных шагов, к которым можно было бы применить систему целых чисел. Те, кто знаком с математикой, несомненно, поймут меня намного лучше, но сейчас я обращаюсь иск­лючительно к разуму. Ниже черты движение дискретно. В этом и заключается сущность сознания, его неотъемлемое свойство: я отличен от вас, я отличен от всего остального Выше этой линии возникает ощущение подвижности лю­бого элемента, непрерывного перетекания одного в другое, Я воспользуюсь символом бесконечности: ∞ потому что по другую сторону от этой черты сознание ощущается как поток — течение, лишенное каких-либо дискретных частей. Его невозможно классифицировать и разложить по полочкам. Кажется, что все непрерывно про­текает сквозь все прочее. Там царит некая упорядочен­ность, но это не удивит тех, кто знаком с математикой: математический анализ непрерывного пространства под­чиняется определенному порядку. Однако это не тот при­митивный порядок, который свойствен простейшей логи­ке. Эта форма логического развития отличается от логики обычных, конечных взаимосвязей, и все же она подчиняет­ся порядку.

На определенном уровне сталкиваешься с мыслью, ли­шенной формы, мыслью вне понятия. Понятия похожи на облачения таких бесформных мыслей, на их хранилища, но мысль может существовать и без этой оболочки — как чистое содержание! Понятия представляют для нас цен­ность лишь в той мере, в какой указывают на содержание, но они не являются самим содержанием. В таком сознании содержание высвобождается из облекающих его понятий и движется как поток. Если вы хотите сформулировать эту идею для объективного сознания, использовать ее здесь, в этом мире, то можете вообразить себе сложный поток, все части которого беспрерывно меняются. Составлять поня­тийное представление об этом —все равно что делать поперечное сечение такого потока: если полученное понятие и справедливо для данного мгновения, то оно окажется не­верным для всех других мгновений, ведь поток постоянно меняется. И это лучшее, чего вы можете добиться.

Концепции, входящие в шастры и сутры [12], предс­тавляют собой попытки описать сечения того, что является потоком. В результате, невзирая на то, что любые подлин­ные сутры, шастры и другие священные тексты действи­тельно открывают истину, они одновременно искажают и обманывают. Все священные писания лишь указывают на истину, которая не может быть облечена в форму, понятие или символ; на истину можно только намекать. Шастры, сутры и священные писания можно использовать только как дорожные указатели, однако люди чаще всего ведут себя совершенно иначе. Вы на каждом шагу видите беды, вызванные теми, кого мы обычно называем религиозными людьми. Они говорят: «Вот мертвая буква Писания, это истина; поскольку у меня есть истина, я уже достиг своей цели». Они похожи на человека, который едет в Юму⁴, добирается до первого дорожного знака со словом «Юма» и указательной стрелкой, выбирается из машины и обнимает этот столб с радостным криком: «Я добрался!» Именно так поступает большая часть людей, и поэтому религия неред­ко становится серьезной преградой. Разумеется, это совер­шенно подлинная вера, а религиозные положения непре­ложны. В этом нет ничего плохого. С ними приходится соглашаться — но застывшие догмы не содержат истину. В этом мнении я совершенно категоричен! Догма в лучшем случае указывает путь к истине, то есть к Осознанию вне слов и форм. Для этого и нужны Писания. Будда, величай­ший из великих, был сторонником чистоты. Он отказывал­ся идти на компромисс, понимая, что никакое слово, ника­кая форма не способны описать ту Действительность, кото­рая открылась ему в Просветляющем Осознании. Он отка­зывался говорить что-либо о содержании этого Просветле­ния, он рассказывал только о тех средствах, которые помо­гают его достичь. И он был прав, совершенно прав, но ограниченному человеческому сознанию это не помогло. Все обернулось великой ошибкой.

Вот одна мысль, которая вновь и вновь повторяется в буддийских сутрах. Я изложу эту идею в понятиях одного из приложений математической логики. Пусть пара А и не-А представляет собой наблюдаемую вселенную (рис. 4). С одной стороны находятся все явления и свойства, кото­рые относятся к «А», а с другой — все то, что «не-А» [13]. Это деление на два множества. Логика утверждает, что лю­бое явление относится либо к «А», либо к «не-А». К приме­ру, любой предмет либо белый, либо нет. Вы с этим соглас­ны, не так ли? Любой поступок может быть либо правиль­ным, либо неправильным. Представление о том, что нет ничего, кроме А и не-А, называется в логике законом иск­лючения третьего. Однако в буддийских сутрах вы столкне­тесь с тем, что отрицается не только А, но в то же время и не-А. О чем это говорит? Действительность не является ни неким понятием — каким бы это понятие ни было, — ни тем, что представляет собой отрицание этого понятия. Что ж, и это верно. О действительности нельзя мыслить исходя из двойственных понятийных представлений. Однако к ка­кому выводу чаще всего приходят люди? К еще одному возможному смыслу, а именно к полному уничтожению — к абсолютной пустоте. Они начинают считать, что оконча­тельная действительность Нирваны сама по себе представ­ляет не что иное, как уничтожение, полное отрицание, сос­тояние отсутствия чего бы то ни было. Сегодня можно услышать, что многие буддисты ведут очень правильный образ жизни ради того, чтобы достичь полного исчезнове­ния. Но это совсем не то, что имел в виду Гаутама Будда [14]. Говорят, что он вернулся еще раз, чтобы исправить возникшее неверное понимание, и воспользовался этим возвращением для передачи метафизических знаний, сми­рившись с неизбежным искажением как с меньшим из двух зол.

РАССМАТРИВАЕМАЯ ВСЕЛЕННАЯ Рис.4

Мне известно, что существуют такие реальности, что для правильного высказывания о них пришлось бы гово­рить «ни А, ни не-А», — хотя и это не помогает выразить их сущность. И все же мы можем найти то, что не входит ни в один из этих классов. А и не-А —наблюдаемая вселенная, и в эти множества не входит тот, кто ее рассматривает. Понимаете, в чем тонкость? Вот она, наблюдаемая вселенная, прямо передо мной. Да, разумеется, она включает в себя мое тело. Этот организм относится к А либо к не-А. Разум также входит в одно или другое множество. Все, чему есть название, можно отнести к А или к не-А. Однако остается окончательный наблюдатель — то, на что мы часто указы­ваем словами я, личность, субъект, но не можем ни опреде­лить, ни назвать подходящим именем; это он, наблюдатель, осознает разделение на Л и не-А, но сам не входит ни в одно из этих множеств. Итак, у нас есть доказательство. Будда совершенно прав. Такие два множества включают в себя не все — и это говорит о чем-то чрезвычайно фундаменталь­ном.

Лекция 2

Что такое раджа-йога [1]? Это особая форма йоги, сход­ная с хатха-йогой [2], но не тождественная ей. Раджа-йога имеет дело главным образом с определенными психи­ческими процессами и отчасти — с процессами физически­ми. По характеру ее правильнее считать неким средством, а не одной из основополагающих Тримарг, к которым отно­сятся пути знания, любви и действия, то есть воли.

Существует ли такое явление, как интегральная йога? Думаю, да. Конечно, это понятие прежде всего связано с именем Шри Ауробиндо [3]. Основная мысль заключается в том, что достижение цели только одним путем может оказаться не достаточным, не очень полным, и потому луч­ше идти по тройному пути, Тримарге, — одновременно либо последовательно. Мне не известно, насколько дейс­твенна интегральная йога, но в самой идее, несомненно, нет ничего плохого.

Можно ли причислить Шри Ауробиндо к тем, кого называют Просветленными? Что ж, я склонен считать его одним из таких людей. Я не берусь оценивать его величие, равно как и величие любого другого Озаренного, ведь если вершины гор скрываются за облаками, нет смысла пытать­ся угадать их точную высоту. Обычно, когда человек утвер­ждает, что такой-то и такой-то — величайший из всех (ра­зумеется, этот такой-то неизменно оказывается самым близким для говорящего), в этих словах отражается эго: «Мой Господь, мой учитель, мой гуру». Когда подчеркивается «мой», а затем следует «самый великий», значит, мы име­ем дело с утонченной формой эгоизма. Не пытайтесь оце­нивать величие тех, кто вышел за пределы земного поля зрения. Достаточно сказать, что любой из них способен озарить нам Путь.

Еще один вопрос: «Что не относится ни к А, ни к не-А?» Самый простой ответ: «Полнота Просветления». Такое от­рицание того, что искомое неизбежно окажется либо в А, либо в не-А, означает, что двойственное сознание не спо­собно его постичь, что предмет поиска выходит за рамки подобных ограничений. Наши рассуждения о наблюдаемой вселенной достоверны только в пределах двойственного сознания. В этом-то и сложность. Вы можете сказать: «Я не могу представить себе иное сознание, нечто другое». Да, совершенно верно. Разве ограниченное, двойственное соз­нание способно вообразить отсутствие двойственности? Дорога к нему проходит через Осознание, а после Осознания вы поймете. До Осознания вы еще ничего не понимаете. Не стоит даже пытаться определять ТО, что находится за лю­быми границами. Определения применимы только в мире двойственного сознания, но наши концепции не пригодны для ТОГО, что кроется за любыми пределами, и только при искусном обращении они могут дать легкий намек на ТО.

Следующий вопрос: «Неужели материя не является из­менчивой?» Этот вопрос вызывает множество встречных вопросов и приводит к трудному положению. Что вы пони­маете под словом «материя»? Вы имеете в виду распростра­ненную гипотезу о слиянии в единое целое всех впечатле­ний, возникающих благодаря органам чувств? Быть может, вы гипостатируете [4] то, что познаете посредством ощущений — осязания, зрения, слуха, давления, кинестетичес­кого напряжения? Нам известно только это. Возможно, вы гипостатируете нечто существующее во внешнем мире не­зависимо от сознания в любом смысле этого слова, то есть нечто лишенное сознания? Если так, то как вы об этом узнали? Нам доступны только ощущения, ничего более.

Я еще не пользовался словом «материя». Я упомянул о двух функциях, органах или свойствах познания, а именно о чувственном восприятии и умозрительном постижении. Мы знакомы только с их деятельностью. Это нам известно, но разве эти способности могут принести сведения о чем-то таком, что пребывает вне любого сознания? Мы привыкли считать, что так оно и есть, но это беспечность мышления. Если вы прочтете буддийские сутры, то заметите, что они очень точно рассказывают об этом. Будда говорил... во вся­ком случае, утверждается, что он говорил так: «Качества — вот все, что у нас есть». Под «качествами» он понимал прак­тические ощущения. Больше ничего нет. Говоря о некото­ром веществе, которое не воспринимается само по себе, но только обладает какими-то качествами, вы недостаточно точны. Этого вы не знаете. Такая привычка легкомыслен­на. Этот вопрос мог бы увести нас на очень зыбкую почву, и я намерен поговорить об этом позже, после определенной подготовки, так как здесь вы сталкиваетесь с проблемой, которая долгие годы занимала философов.

По правде говоря, хорошо осведомленный современ­ный ученый никогда не делает метафизических допущений о природе материи. Я имею в виду по-настоящему разум­ного ученого, а не простого клерка от науки, решающего задачи. Я говорю о людях уровня Эйнштейна [5] или, скажем, Ванневера Буша*. Они понимают, что имеют дело с неким набором определений, пригодным по большей части только для математических формулировок. Опираясь на свои эксперименты, они выдвигают определенные гипоте­зы, благодаря которым эти опыты складываются в целост­ную концепцию. Подобные гипотезы оказываются хоро­шими, если приводят к таким дальнейшим экспериментам или наблюдениям, которые согласуются с гипотетическими предсказаниями и тем самым их подкрепляют. Эти гипоте­зы терпят крах, если не подтверждаются на практике. Один мой знакомый, физик-теоретик, высказал нечто очевидное для каждого математика: любое явление допускает потен­циально бесконечное многообразие возможных объясне­ний. Я попробую вновь использовать математическую ана­логию, чтобы прояснить эту мысль.

рис.5

Одним из простейших и прекраснейших примеров в истории науки может служить то, как Кеплер [6] выявил закон движения планет благодаря наблюдениям Тихо Браге [7], то есть определил, что орбиты обращающихся вокруг Солнца планет имеют почти эллиптическую форму.

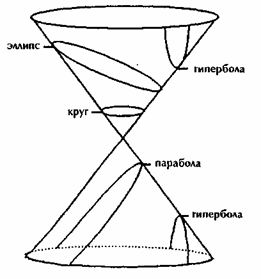
Рис.6

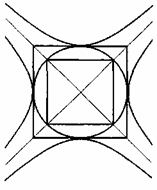
В данном случае, если говорить о пространственных измерениях, он добился достаточно точного результата. Ес­ли вы знакомы с коническими сечениями (см. рис. 6) или уравнениями второй степени, решениями которых могут быть окружность, эллипс, парабола, гипербола или две пе­ресекающиеся прямые, то вам известен и тот факт, что произвольные пять точек однозначно определяют одно из конических сечений.

В данном случае наблюдения показали, что орбиты планет действительно являются эллипсами, хотя и очень близки к окружностям. Несмотря на это, пример послужит неплохой иллюстрацией.

Предположим, некое уравнение описывает выбранную вами гипотезу, постулированное толкование. Если вы нало­жите ограничение, требующее, чтобы решением была кри­вая второй степени, то пять точек будут определять ее од­нозначно. Но что позволяет вам накладывать такое ограни­чение на результаты наблюдений?

Перенесем этот пример на любые результаты наблюде­ний при решении научной задачи. Неужели решением не может оказаться кривая высшей степени, не обязательно второй? Кривые бывают третьей, четвертой, пятой, n-ой степени, их количество бессчетно, и потому можно найти в буквальном смысле бесконечное число кривых, проходя­щих через те точки, которые получены в результате наблю­дений. Таким образом, теоретически возможно построить гипотетическое толкование или теорию, которая объяснит любые факты научных измерений.

Кроме того, ученые навязывают гипотезам определен­ные произвольные правила, которые не объясняются тре­бованиями чистой логики; в частности, гипотезы должны носить такой характер, чтобы они допускали дальнейшую проверку — эксперименты или наблюдения. Это называют требованием операционности. Но можем ли мы быть уве­рены в том, что природа окончательной истины позволит подвергнуть ее проверке с помощью методов двойственно­го сознания? Наука предлагает только прагматическую проверку истинности, а не проверку истины как таковой.

Под словом «прагматическая» я понимаю только то, что она работает, что такие гипотезы приводят к опытам, ре­зультаты которых можно предсказать. Например, если вы повернете ключ зажигания, мотор машины заработает. Нечто предсказанное становится правдой. В практическом, прагматическом смысле вы действительно осуществили проверку. Вот и все. Тем не менее истина, справедливая в мире двойственного сознания, совсем не обязательно дол­жна быть окончательной истиной, то есть истиной как та­ковой, истиной в себе.

Эйнштейн прекрасно сознавал это и говорил об этом. Одним из тех, кем он больше всего восхищался, был сэр Исаак Ньютон [9], чей философский взгляд на природу мироздания Эйнштейн же и опроверг. Он оказался на шаг впереди Ньютона, так как тот еще верил в метафизическое существование и ввел его в свои гипотезы. Он пользовался концепцией абсолютного времени, равномерно пронизы­вающего пространство, но при внимательном рассмот­рении выяснилось, что эта идея не имеет практического смысла. Многие законы Ньютона справедливы. Они по-прежнему выполняются для большинства повседневных явлений, в мелких масштабах, но уже не действительны — нам известно, что они просто не выполняются, — когда мы имеем дело со скоростями, близкими к скорости света, или с огромными, космическими масштабами, — с такими из­мерениями, которые были просто невозможны в эпоху Ньютона. Итак, Эйнштейн говорил, что законы Ньютона были первым приближением к истине, а то, что сделал он, Эйнштейн, с точки зрения огромного опыта науки являет­ся лишь вторым приближением, после чего могут вновь возникнуть очередные изменения. Он прекрасно понимал, что эти открытия были только первыми приближениями в бесконечной последовательности шагов, ведущих к истине. Вот пример скромности подлинно великого научного ума, осознающего ограниченность собственных методов.

Одним из наиболее примечательных признаков шага, разделяющего Ньютона и Эйнштейна, стало то, что теперь в картину мироздания вошла эпистемология*. Те способы, посредством которых мы определяем некий факт, напри­мер световой сигнал звезды, обусловливают форму знания. Таким образом, знания относительны и определяются ог­раничениями процесса познания. В сравнении с прежним объединяющим подходом эта позиция отличается боль­шей зрелостью. Во времена Ньютона она была невозможна, так как тогда человек еще не прозрел и не осознал ограни­ченности собственного процесса познания; это случилось позже. Мы заперты в рамках этой двойственной системы, в пределах ограниченных средств постижения. Как я уже го­ворил, есть две формы познания: чувственное восприятие и умозрительное постижение —то постижение, которое свя­зано с понятиями и концепциями определенного характе­ра.

Именно об этом я говорил вчера вечером. Я не упоми­нал о материи, когда рассказывал о пространстве ниже на­черченной линии, когда отождествлял ее с дискретным соз­нанием, то есть с многообразием отдельных элементов, каждый из которых связан с соседними, как обычные це­лые числа. Затем я воспользовался идеей непрерывного пространства, чтобы описать то, что находится выше этой черты, за пределами двойственного сознания. При этом я построил лишь приближение к истине, поскольку в конеч­ном счете это непрерывное пространство также дискретно, оно тоже отмечено ограниченностью нашего процесса поз­нания.

Элементы-песчинки должны быть достаточно неболь­шими. Вообще говоря, они становятся невероятно крошеч­ными — такими, что их можно назвать «бесконечно малы­ми». Эту мысль оставил нам Лейбниц, и она стала основой дифференциального исчисления — во всяком случае, в мое время. Мы сталкиваемся с понятием бесконечно малых — в буквальном смысле слова бесконечно малых элементов, совокупность которых образует непрерывное пространс­тво. Однако, поскольку это все-таки отдельные песчинки, такое пространство уже не является чистым потоком.

Математики так и не смирились с мыслью о существо­вании чего-то бесконечно малого, ускользающего от лю­бых измерений; эта идея никогда их не удовлетворяла. Го­ворят, что Вейерштрасс [10] полностью отказался от беско­нечно малых. Он считается одним из величайших мыслите­лей в математическом анализе; этот человек интересен уже тем, что писал как поэт. Ему приписывают такие слова: «Математик, в котором нет ни капли поэта, — не настоя­щий математик». Возможно, эта фраза поможет вам полу­чить определенное представление об этом человеке. Он, так сказать, избавился от бесконечно малых, но дорогой ценой. Расплатой стал отказ от существования такого явления, как движение; он пришел к тому, что есть только тела, непод­вижно покоящиеся в определенных точках пространства в каждый отдельный момент времени. Такое представление работает. Опираясь на него, можно построить дифферен­циальное исчисление. Лично я не знаком с его выкладками. В мое время они не входили в курс дифференциального исчисления. Наука пошла по пути Лейбница, и теперь вы имеете полное право считать бесконечно малые элементы чем-то совершенно реальным.

Избавиться от бесконечно малых можно, но при этом придется отбросить представление о существовании само­го движения: останутся только тела, занимающие в различ­ные мгновения определенные положения в пространстве. Интуиция заставляет задать вопрос: «Каким образом мож­но оказаться в ином положении, не перемещаясь в него?» Выяснилось, что такое интуитивное недоумение не так уж обосновано. Достаточно предположить, что то явление, ко­торое называют движением, сводится к неподвижному по­ложению материи (или тела) в разных точках пространства в определенные моменты времени. Это можно назвать ки­нематографическим подходом к действительности, в рам­ках которого идея движения превращается просто в иллю­зию, майю. Я не отстаиваю эту точку зрения, я просто опи­сываю ее. Сейчас я занимаю некую промежуточную пози­цию. Нам известно, что последовательность неподвижных картинок способна вызвать иллюзию движения. Мы стал­киваемся с этим всякий раз, когда приходим в кинотеатр. Каждый образ, возникающий на экране, совершенно ста­тичен, просто кадры сменяются очень быстро, и в результа­те возникает впечатление потока, движения, хотя на самом деле никакого движения нет.

Был один греческий философ по имени Парменид, и он уже в давние времена утверждал, что движения не существует. Его противником был Гераклит [12] — тот са­мый, который сказал, что в мире царит такое движение, что в одну реку нельзя войти дважды — впрочем, это невоз­можно сделать даже один раз. Зенон [13], ученик Парменида, развил его лучшие парадоксы с единственной целью: продемонстрировать, что, допуская существование движе­ния, можно оказаться в очень сложном положении. Он описал знаменитый парадокс состязания Ахилла и черепа­хи в беге, где животное получает определенную фору в рас­стоянии (см. рис. 7).

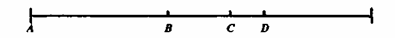
Рис.7

Зенон утверждает, что Ахилл никогда не догонит ее, как бы он быстро ни бежал и как бы медленно ни ползла черепаха. Предположим, Ахилл начинает бег с точки А, а черепаха — с точки В. Чтобы догнать ее, Ахиллу необходи­мо достичь точки В, но тем временем черепаха уже допол­зет до точки С. Это значит, что теперь Ахиллу придется добежать до точки С, но к этому времени черепаха уже окажется в точке D. Это будет продолжаться бесконечно, а Ахиллу потребуется бессчетное число шагов. Совершить бесконечное количество движений за конечное время не­возможно. Таким образом, движения нет.

Это может показаться смешным, но логики и матема­тики сражались с этой задачей более двух тысячелетий и до сих пор не нашли вполне удовлетворительного решения. В нашем мыслительном процессе определенно существуют какие-то серьезные изъяны. Бертран Рассел [14] считал, что решение кроется в том, что за конечное время все-таки можно совершить бесконечное число шагов, так как сумма бессчетного количества элементов не обязательно беско­нечна, она может быть и конечной. Не исключено, что ре­шение существует, но если так, то нам все же придется ждать до тех пор, пока кто-нибудь его найдет. Так что не смейтесь над Зеноном. Он изложил свой парадокс в виде шутки, но сама задача оказалась серьезным испытанием для мышления.

Этим вечером я собирался заняться математической стороной вопроса, но сначала я хочу сказать, что попыта­юсь объединять систематический план лекций и непредви­денные порывы. Систематичность вполне нормальна для обычного интеллектуального построения. Она свойственна лекции любого профессора. К ней относится то, что ты собираешься сделать, причем знаешь об этом заранее. Для этого достаточно подготовки. По этой причине я отношусь ко всему систематическому только как к мелкой подроб­ности: «Я буду говорить об этом тогда-то и тогда-то, а это понятие введу тогда-то» — и этого достаточно, чтобы про­честь лекцию. В противоположность этому, импровизация представляет собой нечто возникающее откуда-то извне, проникающее сверху, из пространства по другую сторону от черты, и никакие способности нижнего пространства не позволят предсказать: «И тогда я скажу это». Импровиза­ция приходит как дар, если вообще приходит. Но когда это случается, ты отбрасываешь всю систематичность в сторо­ну, непредвиденное оказывается сильнее. Сохранять равно­весие между этими двумя силами — очень сложная задача. Может статься, ты вообще забудешь о плане своей лекции, как только она начнется. Такое со мной тоже случалось.

Сделав шаг от двери к кафедре, я забывал обо всем и начи­нал без всякой подготовки говорить на совершенно другую тему — это значит, что я мог говорить целый час, а план рассказа возникал во время самой лекции. Предсказуемо лишь то, что подобное может случиться. Нельзя сказать: «Я скажу то-то и то-то». Когда это происходит, возникает не­кое явление. Под словом «явление» я подразумеваю те осо­бенности, которые могут быть распознаны, обнаружены — во всяком случае, некоторыми людьми. Сознание по ту сторону от черты, то есть за покровом, предстает перед нами в виде Полевого Сознания. Оно может ощущаться как нечто расширяющееся, как осязаемая тишина с лишен­ным формы содержанием. Оно способно взять верх над указаниями умозрительных построений. Когда такое про­исходит, оно захватывает власть твердой рукой, и человек может сделать то, на что обычно не способен. Оно может вызвать у тех, кто оказался рядом, мистические пережива­ния — радостные состояния сознания, чувство счастья. Оно может вызвать ощущение жара — логичных поясне­ний этому нет, но это бывает. Ошибка исключена. Я видел, как лица становятся румяными, как они покрываются ис­париной, а люди начинают снимать пиджаки. Результаты бывают очень ощутимыми, а сам человек может произно­сить слова так, что они становятся приказаниями не только для него, но и для всех остальных.

Где источник подобных знаний? Он не один. Часть этих сведений может приходить из глубин незримой сторо­ны самого человека. Она может быть познаниями Братства, так как это Братство представляет собой многих в одном — это не совокупность отдельных песчинок, а единое целое, которое можно описать таким образом: «я» превращается в «мы», одновременно оставаясь «я». Выше и ниже этих зна­ний простираются мысли, которые не принадлежат какой-либо личности — знания, не требующие познающего, нечто вроде Всеобщего Хранилища. Это та сила, которая способ­на менять сознание человека, переносить его ближе, приб­лижать к отверстию вверху. Возникнув, такое состояние начинает главенствовать над всем прочим. Оно может ца­рить некоторое время, а потом уйти. В таких случаях я вновь возвращаюсь к систематичности. Спонтанные отс­тупления не следует считать личной прихотью говорящего, это результат совместных усилий выступающего и слуша­телей. Они никогда не случаются, если ты окружен неблаго­желательной аудиторией или теми... ну, например, теми, кто думает: «Кем этот парень себя воображает?» Все зависит от внутренней связи. Для поисков такой связи часто требу­ется время, но это возможно. Эти состояния могут быть очень глубокими, почти такими же мощными, как самадхи [15] во время бодрствования.

Это крошечный проблеск чего-то Запредельного. Заг­лядывая в эти глубины, относительное сознание может сна­чала счесть их тьмой, безмолвием и пустотой. Однако при смещении на их собственный уровень, при переходе к ино­му способу постижения они воспринимаются как необы­чайно яркий свет, как полнота и вершина содержательнос­ти — как внутренняя сущность звучания. По существу, это происходит и сейчас...

Помнится, я сказал, что мы перейдем к вопросу опре­делений. Давайте переключаться. Что такое математика во­обще? Название моих лекций: «Математика, философия и йога». Такое сочетание тематик имеет свои причины. Это тот путь, которым я шел, и потому я лучше всего знаком именно с ним. Если вы обратитесь к различным справочни­кам, как сделал я, то найдете в них множество разнообраз­ных определений того, что понимается под математикой. Я нашел одно из них в «Сэнчери Дикшнэри», где математика определяется как «наука о количестве» [16]. Кажется, такое представление очень широко распространено, но оно оста­ется чрезвычайно далеким от истины. В математике есть много областей, не имеющих ничего общего с количествен­ными отношениями — например, алгебра логики, творе­ние великого ирландского ученого Буля, которого Рассел назвал первым чистым математиком. Алгебра логики не связана с количеством, она рассматривает классы, множес­тва, взаимоотношения между ними и прочие подобные вопросы.

Другим примером направления, никак не связанного с вычислениями, — кстати, очень красивым направлением, — является проективная геометрия. Думаю, пример из этой области покажется вам занятным. В проективной гео­метрии вообще не рассматриваются метрические свойства, в ней не используются измерения. Понятие меры является основополагающим во всем, что касается количества, но проективная геометрия занимается описательными свойс­твами. Начертим две произвольные прямые и назовем их L и L’ (см. рис. 8).

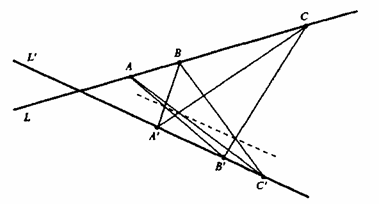
Рис.8

Выберем на каждой прямой по три произвольных точ­ки. Обозначим точки на прямой L буквами А, В и С, а точки на прямой L' —А', В' и С’. Теперь соединим отрезком точки Аи В', а также пару А' и В. Отметим место пересечения этих отрезков. После этого построим отрезки, соединяющие па­ры точек В и С', С и В', С и А' и, наконец, С' и А. Помните, что прямые и все точки были выбраны совершенно произ­вольно, мы не прибегали к каким-либо измерениям. Кроме того, прямые вообще бесконечны. В проективной гео­метрии все прямые имеют бесконечную длину, так как опе­рации с ними не связаны с измерениями. Длины и углы не имеют никакого значения. Эта теорема (первым ее доказал Паскаль [17], и она является частным случаем более общей теоремы о конических сечениях) заключается в том, что три полученные точки пересечения построенных отрезков лежат на одной прямой. Математику такой результат ка­жется очень красивым —и не потому, что его можно уви­деть воочию, а по той причине, что он оказывается полной неожиданностью. Вся изюминка в том, что это справедливо для любых, самых произвольных прямых. Точки также вы­бираются произвольным образом — вы можете поместить их куда пожелаете. Вы просто чертите прямые L и L', прово­дите три соединяющих их отрезка — и обнаруживаете, что полученные точки пересечения находятся на одной пря­мой. Если вы ощутили это, то получили определенное пред­ставление о той красоте, которую ценят математики. Это умозрительная красота. Она заключается в том, что между элементами, которые казались независимыми, разрознен­ными, внезапно возникает некое единство. Подобные пере­живания случаются часто, но обычно осознаются только при высоком уровне сосредоточенности, способном вызы­вать экстатическое состояние.

Более полное и точное определение математики приво­дится в «Словаре философии и психологии» Болдуина. Там сказано, что «математика представляет собой науку об абс­трактных отношениях» [18]. В своей статье для девятой редакции «Британской энциклопедии» Уильямсон гово­рит, что «любая концепция, полностью описываемая ко­нечным набором определений, является математическим понятием» [19]. Кроме того, Рассел сказал, что чистая мате­матика представляет собой класс всех утверждений в форме «р влечет q», где р и q являются утверждениями, содержа­щими один и тот же набор переменных и не включающими в себя никаких постоянных, кроме логических констант.

Вернемся к неметрическим областям математики. По­мимо алгебры логики и проективной геометрии, существу­ет топология, которую иногда называют «геометрией на резиновой плоскости». Это чрезвычайно важное направле­ние. Топология изучает те отношения, которые остаются неизменными при любых деформациях пространства. Ска­жем, плоскость можно растянуть таким образом, чтобы квадрат превратился в круг, а эллипс — в любую другую фигуру. Что же останется неизменным? Связность отдель­ных частей. Подобные опыты приводят ко множеству за­нятных построений — например, к созданию односторон­ней поверхности —ленты Мебиуса (см. рис. 9).

ЛЕНТА МЕБИУСА

Рис.9

Если вы перекрутите бумажную ленту ровно один раз, а затем склеите ее концы, то сможете, не отрывая карандаш от бумаги, провести вдоль центральной оси этой ленты одну прямую, которая протянется по обеим сторонам и вернется к исходной точке без необходимости изменения направления движения на обратное.

Порой люди занимаются исследованиями очень стран­ных вещей, многие из которых чрезвычайно далеки от воп­росов, связанных с измерениями.

Мы приближаемся к тому вопросу, который выходит за рамки любых определений, — к вопросу об основопола­гающей сущности математики. В ней выделяют три общеп­ризнанные школы. Одна из них известна как логицизм, и самым видным ее представителем был Рассел. Логицисты считают, что математика — это только логика. Они при­держиваются представления о том, что всю ныне извест­ную математику и любые математические направления, ко­торые могут возникнуть в будущем, можно свести к чисто логическому процессу (такому процессу, который можно использовать для программирования технических уст­ройств). Сделать это пока не удалось. Логицизм сталкивает­ся со множеством трудностей, с очень серьезными парадок­сами. Например, представим себе множество всех мно­жеств, которые не являются собственными элементами. Входит ли такое множество само в себя [20]? В свое время этот вопрос, то есть задача, был направлен в адрес Пеано [21], который только что завершил двухтомный труд по математической логике. Книга уже была в типографии, но этот вопрос полностью обесценивал ее содержание. Пеано сказал: «Как трудно смириться с тем, что после долгих лет, посвященных научным исследованиям, воздвигнутая вами башня разваливается в один миг». Вы можете сами убедить­ся в том, что на такой вопрос нельзя ответить ни «да», ни «нет». Этот парадокс возник в рамках самого взгляда на природу математики. Я задумываюсь о том, не попытались ли логицисты сделать ее чрезмерно чистой — в том смысле, что практически отказались от интуиции и свели математи­ку к логическому процессу, который не пользуется интуи­цией и не испытывает в этом потребности.

Сейчас я попытаюсь подвести всему этому итог. Мно­гие из вас еще не понимают, к чему я веду, но в действитель­ности мы говорим о силах и слабостях, ограничениях чис­того мышления, — а такое чистое мышление проявляется именно в математике. Поэтому я надеюсь, что вы не по­жалеете о потраченном на понимание этих примеров вре­мени — даже те из вас, у кого нет особых познаний в мате­матике. Кроме того, подобные рассуждения отчасти подго­товят нас к некоторым возможным трудностям.

Другой школой математики является формализм, свя­занный, в частности, с Гильбертом [22]. В отличие от шко­лы Рассела, формализм уделяет особое внимание не логике, а необычным формам геометрии. Когда Евклид [23] писал свои труды по геометрии, он воспользовался рядом пред­положений, которые назвал «аксиомами», то есть «само­очевидными истинами», чем-то таким, в правильности че­го никто не сомневается. В действительности, Евклид пред­ставил их в форме постулатов, а не обычных определений (аксиом) [24]. Он начал с этих положений и вывел из них все остальное. Пятая аксиома, известная как аксиома о па­раллельности [25], выглядит очень сложной. В ней утверж­дается: если сумма двух внутренних углов по одну и ту же сторону от некой прямой, пересекающей две заданные пря­мые, равна сумме двух прямых углов, то исходные прямые не пересекаются (см. рис. 10). Это утверждение кажется похожим на теорему, то есть на нечто требующее доказа­тельства, но на самом деле это аксиома. В современных учебниках вы, вероятнее всего, встретите ее в такой форму­лировке (см. рис. 11): через точку С, не лежащую на прямой АВ, можно провести одну и только одну прямую, парал­лельную прямой АВ. Так ее описывают в наши дни, а пер­вый вариант представляет собой формулировку Евклида. Поскольку она выглядит похожей на теорему, многие мате­матики пытались доказать ее, опираясь на остальные акси­омы, но потерпели полную неудачу.

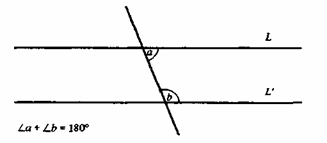
ПЯТАЯ АКСИОМА ЕВКЛИДА

Рис.10

Рис. 11

Следующим шагом стала попытка выдвинуть иные предположения. Лобачевский и Больяй [26] независимо друг от друга допустили, что через точку С, не лежащую на заданной прямой АВ, можно провести по меньшей мере две прямые, параллельные АВ. Это означает, что и прямая CD, и прямая СЕ могут не пересечь прямую АВ —нигде, кроме, быть может, бесконечности. Просто предположим, что это правильно. Быть может, мы так не думаем, но дело не в этом. Можно ли, пользуясь этой аксиомой, построить внутренне непротиворечивую геометрию? Да. И это было сделано. В геометрии Лобачевского многие, практически все, положения Евклида, опирающиеся на аксиому о парал­лельности, выглядят совершенно иначе. Например, все вы знакомы с утверждением о том, что сумма углов треуголь­ника равна двум прямым углам, но в геометрии Лобачевс­кого эта сумма всегда превышает сто восемьдесят градусов.

Другой математик, Риман [27], примерно в те же годы допустил, что через точку С невозможно провести ни одной прямой, параллельной заданной, то есть любая из них неп­ременно пересечет выбранную прямую АВ на конечном расстоянии от точки С. Это уточнение очень важно. В гео­метрии Римана движение по любой прямой в одном нап­равлении непременно заставит вас вернуться к исходной точке с другой стороны. Быть может, это противоречит интуитивным представлениям, но в построении такой гео­метрии тоже нет логических ошибок. Она внутренне неп­ротиворечива.

По мнению Рассела, в математике допустимы любые внутренне непротиворечивые концепции. Это значит, что геометрии Лобачевского и Римана имеют право на сущест­вование. Через полсотни лет после Римана родился Эйн­штейн, который развил общую теорию относительности. Обнаружив, что его концепция мироздания соответствует Римановой геометрии, Эйнштейн сказал: «Как могло слу­читься, что заточенного в башне из слоновой кости матема­тика посещают совершенно правильные мысли о строении внешней вселенной?» Это очень хороший вопрос. Такого чистого математика, как Риман, интересует прежде всего, так сказать, интеллектуальное упражнение. Это относится ко всем чистым математикам. Подобно богам, они не руко­водствуются исключительно чувством долга. Математик делает нечто только во имя удовольствия. Такой образ жиз­ни ведут все вольные души, и математики показывают нам огромное число примеров такой свободы. У вольной души нет обязанностей. Она делает что-то совершенно спонтан­но, однако такие непреднамеренные действия почти всегда приводят к блестящим результатам. Да, чистый математик запирается в башне из слоновой кости и мыслит только ради удовольствия. После этого кто-то из проходящих ми­мо берет его результаты и обнаруживает, что они предлага­ют власть над той или иной сферой природы. Однако это вызывает у чистого математика боль, так как милая его сердцу чистота оказывается запятнанной практическим применением.

Рассказывают, что один математик, у которого возник­ла совершенно непрактичная идея, воскликнул: «Слава Бо­гу, что эта мысль не имеет никаких вообразимых сфер при­ложения». Разве это странно? Что почувствует художник, если напишет прекрасную картину, а потом некто отберет ее и начнет использовать для продажи «кока-колы»? Те же чувства охватывают и чистого математика. Не все мы слеп­лены по одному образцу. Вот простой факт: практически все математические творения были созданы чистыми мате­матиками, запиравшимися в башнях из слоновой кости; к тому же всем нам известно, что любые попытки творить ради практической пользы делают творчество невозмож­ным. Единственным исключением стала развитая Ньюто­ном теория производных, то есть дифференциального исчисления. Ньютона занимали концепции мироздания, а математика оставалась для него лишь инструментом. То же самое можно сказать и о значении математики для Винера [28], одного из главных теоретиков в области создания вы­числительных машин в наши дни. Он был склонен зани­маться не чистой, а прикладной математикой.

Поговорим об этом подробнее. Вот история о Рамануджане [29], величайшем восточном (индийском) математи­ке моего времени, и об английском ученом Харди [30]. Оба были чистыми теоретиками. На одной из своих лекций Харди рассказывал о том, как нанял кэб и отправился на­вестить Рамануджана, когда тот гостил в Англии. Появив­шись, Харди сказал: «Я приехал на кэбе номер 1729 — очень скучное число». Его друг-индиец возразил: «Напротив, это очень интересное число. Это минимальное из всех чисел, которые можно двумя различными способами представить в виде суммы двух кубов». Попробуйте самостоятельно найти решения этой задачи [31].

Дело в том, что вольная душа не трудится, а играет. Действия такого человека представляют собой спонтанное проявление радости, но такой подход приводит к величай­шим открытиям. Что касается расцвета формализма, кото­рый начался после развития неевклидовых геометрий, то этот подъем стал подлинной революцией в представлениях о природе математики. Была низвергнута сама идея аксиом, то есть убежденность в существовании неких несомненных истин, на основе которых выстраиваются логические рас­суждения. Вместо аксиом у математиков осталось только то, что можно назвать «основополагающими исходным