Драматическая Вселенная, Том 1

КНИГА ВТОРАЯ:

ЕСТЕСТВЕННЫЕ НАУКИ

Часть пятая

МИР ДИНАМИКИ

Глава 13

ПРЕДСТАВЛЕНИЕ ЕСТЕСТВЕННОГО ПОРЯДКА

5.13.1. ЕСТЕСТВЕННЫЙ ПОРЯДОК

В течение сотни поколений, со времен халдейских магов, Конфуция, Гаутамы Будды и ранних греческих философов, человек искал разрешение загадки вселенной, руководствуясь одной фундаментальной аксиомой, а именно – утверждением естественного порядка как общего основания всеми разделяемого опыта. Халдеев можно назвать духовными предшественниками современного мира постольку, поскольку они одними из первых утверждали, что явления не произвольны, и пытались сформулировать универсальные законы.

Обычно не замечают, что без утверждения естественного порядка слова "возможно" и "невозможно" не могут иметь значения. Цель естественной философии – не объяснение событий, но формулирование правил, позволяющих отличить возможное от невозможного. Только когда это сделано, мы можем достаточно последовательно устанавливать связь между настоящим моментом с его быстротечностью и кажущимся непостоянством актуализации, и другими моментами опыта, удаленными во времени и пространстве.

Мы определили реальность как тотальность всего возможного опыта и феномены как осведомленность о реальности, как она возникает в конечных центрах сознания. Феномены могут казаться нам произвольными и даже бессмысленными, но это происходит лишь постольку, поскольку мы не видим их в контексте более широкого порядка. Убеждение, что феномены непроизвольны, возникает из уверенности в универсальности естественного порядка. Вера в универсальные законы и надежда найти их усиливалась в течение сотен поколений. Человек, искавший порядок во вселенной, не был разочарован. Существует, тем не менее, предел, дальше которого утверждение естественного порядка как абсолютного и неизбежного идти не может; в законченной схеме – упорядоченной   во всех деталях и, следовательно, с необходимостью предопределенной – ни  свобода, ни ответственность не могут иметь значения.

В мире, управляемом исключительно самосогласованными и неумолимыми законами, самый простой вопрос не только не имеет ответа, но даже и не может быть поставлен. Вопросы возникают как раз потому, что порядок не является всем, но на них может быть дан ответ лишь постольку, поскольку порядок вездесущ. Мы, конечно, задаем вопросы, и мы рассчитываем найти ответы. Следовательно, вся наша философская деятельность основывается на убеждении, что порядок и беспорядок как-то переплетаются в ткани реальности. Если бы вселенная была разделена на две части – упорядоченную и неупорядоченную – эти две части не могли бы быть связаны между собой, и ни одна из них не могла бы быть местом обитания человека. Мы должны, следовательно, сделать вывод, что порядок и беспорядок неразделимы. Естественная философия должна искать регулярности, признавая, что порядок в форме универсальных законов не может распространять свое господство до абсолютного исключения всякого беспорядка без разрушения свободы и ответственности. Различение порядка и беспорядка достигается в процессе прояснения опыта, которое завершается раскрытием детерминирующих условий существования в форме универсальных законов. Результаты этого разделения устанавливают науки о системе координат. Система координат является тотальностью условий, которые предохраняют  вселенную от хаоса, не приводя ее к бесплодности. Законы системы координат раскрываются посредством изучения функциональных аспектов феноменов, то есть поведения. Такое изучение, однако, может превысить возможности нашего мышления, если не упростить его, приняв в расчет относительность существования. Стратификация существования дает нам возможность устранить некоторые из трудностей, вытекающих из различий в уровнях бытия рассматриваемых сущностей, и установить основания, твердо опирающиеся на законы системы координат. Тем не менее, когда мы хотим применить эти законы к какому-либо данному феномену, мы снова должны обратить внимание на разные уровни бытия, потому что слова "возможно" и "невозможно" меняют свое значение в зависимости от уровня сознания, к которому они относятся.

5.13.2. НЕИСЧЕРПАЕМОСТЬ ФЕНОМЕНОВ

Человек постоянно убеждается на собственном опыте, что каждый вопрос, на который ему удается найти ответ, влечет за собой новые вопросы, на которые он ответить не может. Феномены являются нам как из рога изобилия, и как бы много ни удалось человеку извлечь из этого, они все равно переливаются через край вместе с неразрешенными проблемами. Это подсказывает геометрическую аналогию отслаивания двумерных поверхностей от трехмерного тела, которое не уменьшается в толщине, как бы много таких поверхностей мы ни сняли. Реальность имеет большее число измерений, чем мысль, и мы должны научиться приспосабливать наше мышление к признанию его собственной неадекватности.

Философы обсуждали отношение между видимостью и реальностью, причем идеалисты вынесли приговор всему, существующему во времени, как "всего лишь видимости" и считали "реальным" только вневременный, вечный Абсолют. Этот вид идеализма не удовлетворяет нас, но и реализм, трактующий феномены как объективную реальность не убедителен. Мы не может верить, что реальность полностью субъективна, но равным образом мы не можем принять, что она полностью объективна.  Не может быть разделения реальности на две сферы, субъективную и объективную, одну целиком опытную, другую совсем лишенную опыта. Все, что мы обнаружили в первой части наших исследований, должно убедить нас, что любая такая дихотомия ложна. Дуализм, который стремится сохранить обе точки зрения, не стремясь вместе с тем их согласовать, бесплоден, плюрализм же, рассматривающий множественность как окончательную реальность, есть признание неудачи. Даже триада "сознание – функция – воля" взятая отдельно, не принимает в расчет различные степени, в которых эти три элемента сплавляются в ситуациях разных типов. 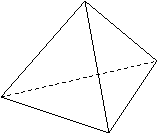Вселенная, как она субсистирует, простирается сквозь множество таких степеней или уровней, так что весь опыт может быть представлен треугольной пирамидой с единством в вершине и множественностью в основании.

                                                 U

                                                                   B

                       F

                                                        W

U - Единство

F - Функция

B - Бытие

W - Воля

Рис.13.1. Единство и множественность.

На диаграмме функция, бытие и воля показаны отдельно в трех вершинах основания, как если бы они были взаимоисключающими компонентами. Каждая точка O внутри треугольника основания представляет сочетание, в котором все три сводятся вместе в определенном отношении. Тогда реализм может быть определен как учение, утверждающее, что не существует ничего, кроме основания пирамиды. Напротив, идеализм, - неизбежно приводящий к монизму,  - утверждает, что только вершина реальна, а все остальное – только видимость. Если принять одну из этих доктрин, в качестве истины, то на любой и каждый вопрос может быть дан окончательный ответ. Однако опыт противоречит обеим доктринам и учит нас, что есть множественность в каждом единстве и единство в каждой множественности; реальность во всяком явлении и явление во всякой реальности. Соотношение явления и реальности меняется от одного опыта к другому в соответствии с наличным состояние сознания. Более того, баланс функции, сознания и воли сам по себе уникален в каждом случае. Другими словами, для представления опыта необходима вся пирамида с ее трехмерным континуумом течек, тогда как наш исключительно ментальный процесс может служить в лучшем случае для создания двумерного, или плоского, представления.

Точки, расположенные на вертикальной оси OU показывают баланс между детерминизмом и свободой. Подобно этому перпендикуляр из точки F на плоскость UBW измеряет соотношение между абстрактностью и конкретностью. Высота, опущенная из вершины В, показывает уровень бытия, а перпендикуляр из точки W к плоскости UFB дает "отношение простоты". В вершине  W есть только один закон, то есть закон свободы, в то время как на плоскости UFB  воля проявлена во всей сложности, которая может возникнуть из относительности бытия и множественности функции. Здесь нет свободы, а только действие механических законов.

Эта схема может быть приспособлена для представления феноменов. Пирамида представляет все возможности, и все, что оказывается вне нее, невозможно и, следовательно, не существует. Реальность по ту сторону существования находится вне области философского исследования.

Сказанного достаточно для того, чтобы продемонстрировать необходимость, по крайней мере, четырех независимых координат. К несчастью, устройство нашего интеллектуального аппарата такова, что мы может "мыслить" только путем сведения феноменов к двучленным комбинациям. Таким образом, мы всегда и неизбежно отрезаны от прямого опыта двух из четырех измерений реальности. Это остается истинным, как бы мы ни выворачивались, поворачивались  и ни стремились найти доказательства противоположного.

Все основные дисциплины изучают одну и ту же пирамиду, но берут в качестве вершины разные точки. Естественная философия стремится к исчерпывающему знанию функции и, следовательно, помещаем пирамиду в положение, показанное на рис.13.2.

В вершине – совершенный порядок вселенной, постигаемый как единый функциональный механизм. В основании с его тремя вершинами – бытием, единством и волей, - представлено все богатство непосредственного опыта с его неразрешимой сложностью и его не упорядоченностью, как реальной, так и кажущейся. Эти три точки основания теперь привлекают внимание к трем фундаментальным постулатам естественной философии, а именно:

Единство – то есть самосогласованность естественного порядка (U)

Система координат – то есть вездесущность универсальных законов (W)

Стратификация существования – то есть постулаты существования (В).

                                                 F

                                                                   B

                        U

                                                        W

Рис.13.2. Естественная философия.

Идеальная ситуация, к которой стремится естественная философия, представлена точкой F, в которой весь возможный опыт проявляется как действие простых, универсальных, самосогласующихся и функциональных "Законов Природы". Только в этой точке вся неопределенность воли и сознания устранена из картины мира.

Человек с его ограниченным восприятием может исследовать лишь малую часть пирамиды и – как мы видели – не может адекватно представить даже то, что он обнаруживает. Мы должны, однако, предположить, что в каждой вершине присутствует тотальный идеально возможный опыт, и некоторое представление о его характере может быть выведено путем устранения трех других компонент из всего возможного опыта. Воля, отделенная от бытия и функции и от фундаментального постулата единства – не  более чем система координат, и мы можем надеяться многое узнать, изучая эту вершину как одно из трех оснований естественной философии.

5.13.3. МАТЕМАТИКА

Поскольку ограничение беспорядка системой координат есть чистое действие воли, мы не можем ни знать ее, ни сознавать, но все же она может быть понята. Мы никогда не обнаруживаем в реальности пространство, время, вечность или гипарксис; мы находим только события, управляемые этими детерминирующими условиями. Если мы пытаемся трактовать детерминирующие условия как объекты знания, мы фальсифицируем их и вводим себя в заблуждение из-за ошибки неуместной конкретности. Например, все дискуссии о природе времени бессмысленны, поскольку время как таковое не имеет ни природы, ни свойств. Мы можем, однако, знать факты, и те регулярности, которые мы открываем как общие для всех фактов, могут быть выражены как законы.

Наше возможное понимание детерминирующих условий весьма отлично от нашего возможного знания факта. Первое возникает из опыта бесчисленных поколений, но мы можем описать в функциональном языке эти условия не лучше, чем рыба могла бы описать воду. Нам необходимо, следовательно, использовать специальный язык, который должен, насколько это возможно, быть свободным от относительности бытия и разнообразия функции, и который выражает только абстрактные действия воли. Язык, обладающий этим свойством абстрактности – это математика.

Часто отмечалось, что существует своеобразное и тонкое соответствие между математическими операциями – которые  кажутся чисто концептуальными и субъективными – и  процессами во вселенной – которые выступают как объективные и несводимые к концептуальным формам. Это тем более примечательно, что анализ математическими средствами не может распутать даже самый простой случай, возникающий в нашем опыте. Язык математики имеет мало ценности, или совсем ее не имеет, при описании факта, и, тем не менее, мы обнаруживаем в нем замечательную способность связывания и объединения субъективного опыта и объективной реальности.

Этот парадокс может быть разрешен, только если мы поймем, что математические символы означают не функциональные действия, но акты воли. Символ  δ∫dS используется при определении пути, проходимого каким-либо телом при консервативном движении в силовом поле, но он не говорит нам, чем является тело или движение, и не описывает какое-либо событие. Рассмотрение таких символов должно убедить нас, что математика занимается единственно разделением возможных и невозможных действий и процессов. Связь не всегда является самоочевидной, но она всегда может быть раскрыта, если мы стремимся понять значение символа или операции безотносительно к какому-либо специфическому факту. Сила математического символизма заключается именно в том, что он дает возможность описывать различные по функциональному характеру действия при помощи одного и того же символа. Более того, математические утверждения всегда имеют дело с возможностью или невозможностью оказий, безотносительно к вопросу о том, была ли или будет ли какая-либо частная оказия актуализирована. С давних времен на человека производило глубокое впечатление соответствие между математическими операциями, которые являются чисто ментальными и очевидно находятся под контролем нашего сознания, и физическими событиями, которые находятся вне нашего ума и не зависят от нашей воли. Математичность объективного мира есть данность, с которой мы должны считаться. Это не означает, что каждая функциональная проблема поддается математической обработке. Напротив, в том и заключается огромная трудность, что лишь малое число весьма специализированных оказий может быть адекватно выражено в математической символике. Тем не менее, мы остаемся убежденными в том, что математика может дать нам проникновение в физический мир, которого мы не можем получить при помощи только чувственного опыта. Более того, мы твердо верим, что за всей сложностью и "нематематичностью" нашего непосредственного опыта находится упорядоченная совокупность частиц и силовых полей, подчиняющаяся строгим математическим законам. Блуждая свободно и случайно в пустых ассоциациях, наши мысли остаются неразрывно связанными с физическими процессами в нашем мозгу, которые, как мы верим, могут быть выражены в терминах символизма математической физики. Необходимо подчеркнуть – и даже особо подчеркнуть – парадокс   универсальной применимости математического символизма и нематематичности чувственного опыта, для того чтобы уяснить себе важность различения между математическими символами как языком воли и вербальными описаниями как языком функции.

Помня, что язык воли характеризуется использованием жестов, каждый из которых имеет уникальное значение в данный момент, мы можем предполагать, что математика имеет качество жеста. Так дело и обстоит. Каждый математический символ соотнесен с некоторым жестом. Например, тригонометрические функции – синус, косинус, тангенс – привлекают наше внимание как к универсальным отношениям в прямоугольных треугольниках, так и к свойствам бесконечных рядов. Было бы трудно или даже невозможно выразить посредством слов или знаков все, что математик узнает в символе π. Она замещает число, которое само по себе уникально, но оно далеко от того, чтобы быть "просто" числом, так как оно выражает все наши представления о кругообразности и повторяемости, делая это с силой жеста, который был столь же полон значения для строителей пирамид, как он значим для современного математика или инженер. Мы, таким образом, привыкли обращаться с π скорее как с оператором, чем как с числом, но часто забываем про это, когда стремимся определить его значение.

Уравнение:

d²ψ / ds² + k²ψ = 0

дает нам формы всех возможных вибраций, то есть событий, в которых возмущающая и восстанавливающая силы находятся в ритмическом равновесии. Это уравнение применимо в бесконечном множестве случаев, и их функциональное содержание не имеет ничего общего с действенностью уравнения. Математик понимает его значение без интерпретации в терминах функции или бытия. В этом заключается особый характер математического символизма, а именно то, что он является языком чистой воли, а не воли, на которую накладывается полное выражение функции и бытия, как в случае "практического языка".[1]  Следовательно, математика в истинном смысле – это язык системы координат, и он является полностью действенным только для угла пирамиды опыта, отмеченного на диаграмме 13.1 буквой W.

В строгом смысле слова математика не может быть "знаема" и недооценка этого является причиной многих трудностей, с которыми сталкиваются в математических исследованиях. Математика никак не касается качественного содержания опыта. Она может описывать, что возможно и что невозможно в ситуации данного типа, но ничего не может сообщить о том, что в этой ситуации "следует" и чего "не следует" делать. Точно также она может сказать нам не что представляют собой вещи, и не в какие оказии они входят, а только – для вещей, являющихся тем, что они есть – возможна ли данная ситуация. Исходя их этого, математика может рассматриваться как характеристический язык естественного порядка.

5.13.4. ПРЕДСТАВЛЯЮЩЕЕ МНОГООБРАЗИЕ

Каждый акт воли устанавливает отношение, и воля, следовательно, имеет особую связь с триадой. Это наводит на мысль, что математический символизм не может быть полон, поскольку он ограничен двучленными комбинациями. Хотя первичными компонентами математики являются элементы (terms) и операции, ее цель достигается только когда они представлены в правильном отношении.

Например, равенство:

S = 2 πR

связывает в правильном отношении оператор π с двумя элементами S и R, представляющими длину окружности и радиус круга на евклидовой плоскости. Утверждение состоит в приравнивании, отрицание – в несоизмеримости этих элементов, и согласование – в универсальном рекуррентном операторе π.

Выражение любой связи между двумя элементами требует отнесения, независимого от самых элементов и операций над ними, иначе мы не имели бы возможности что-либо сказать о делаемом. Эта независимая система отнесения не обязательно должна быть эксплицитной, но если она служит не только для потребностей отдельного случая, она должна каким-то образом соответствовать законам воли. При установлении схемы естественной философии, следовательно, первой является задача выработки средств представления, которые должны иметь, насколько это возможно, универсальную действенность и универсальное значение. Нет другого пути избежать функционального описания, имеющего силу только ad hoc.

Остановимся, чтобы обсудить, что мы имеем в виду под "средствами представления". Предположим, я хочу указать положение нескольких предметов в комнате, где я сижу. Напротив меня, немного выше моей головы, находятся часы на каминной полке; справа от меня в десяти футах у стены стоит стол; под моим стулом лежит на полу ковер. Таким образом, я могу называть и указывать положение какого угодно числа предметов. Действительно, процедура эта настолько знакома, и кажется настолько простой, что мы не замечаем, например, что слова "напротив", "выше", "справа", "ниже" имеют одно и то же значение и для нас, и для тех, кто будет следить за нашим описанием, и в то же время мы знаем, что если бы я повернулся на стуле лицом к окну, то же самое описание потребовало бы перестановки слов. Если бы, однако, я взял за начало отсчета не себя, а камин, слова "перед", "выше", "справа" и "слева" имели бы одно и то же значение, в каком бы положении я ни сидел. Таким образом, мы видим, что на практике мы всегда можем найти и представить фиксированную систему отсчета или систему координат для описания положений. Точно также слова "вчера" и "завтра" меняют свое значение при переходе от одного дня к другому, но "до или после 11-го ноября" означает сегодня то же самое, что означало вчера, и что будет означать завтра.

Средство описания места и времени событий называется представляющим многообразием.[2] Опыт учит нас, что такая схема не ограничивается только описанием, но сообщает нам также что-то о возможном и невозможном. Возможно, что "до" перейдет в "после", пока я спокойно сижу на своем стуле; но невозможно, чтобы "перед" превратилось в "позади" до тех пор, пока я не повернулся. Для меня возможно изменить "здесь" на "там" и "там" снова на "здесь" движением моего тела, но невозможно изменить "сейчас" на тогда" или "тогда" на "сейчас" каким-либо известным мне способом. Точно также геометрия дает мне различную информацию о том, что я могу и чего не могу делать с линейками и кусками веревок; и таким же образом кинематика сообщает мне, какие наблюдения возможно и какие невозможно делать с часами и движущимися телами. Эти рассуждения дают нам возможность различать описание и представление. Теперь мы можем определить слово "представление" как обозначающее акт, посредством которого мы указываем отношение функции к воле в данной ситуации. Поскольку сейчас мы  занимаемся только волей, проявляющейся в форме порядка, мы можем дать более точное определение представления как акта воли, соотносящего поведение с системой координат. Представление, таким образом, рассматривается как особая форма языка, которая пригодна для математической обработки. Оно использует символизм для сохранения общности законов системы координат, но допускает приложение к частным случаям, если только может быть установлен уровень существования.

5.13.5. ГЕОМЕТРИЧЕСКИЕ СИМВОЛЫ

Геометрию обычно рассматривают как науку, в которой мы обнаруживаем и изучаем законы пространства. В более общем смысле ее можно рассматривать как науку о представлении, без каких-либо ограничений только пространство-подобными отношениями. Например, сейчас привычно говорить о четырехмерной геометрии пространства-времени и даже об N-мерной геометрии неспециализированного характера. Мы, следовательно, можем принять термин геометрия для того, чтобы обозначить изучение представления.

Язык математики требует применения чисел, и возникает вопрос, какая степень независимости между различными наборами чисел необходима, чтобы дать адекватное представление о событии. Независимый набор чисел называется измерением /dimension/, а некоторое множество таких наборов мы называем многообразием /manifold/. Одной из задач наук о системах координат является определение наиболее подходящего многообразия для представления всех гипономных сущностей. Каждое целое является – в отношении своей простой целостности – единицей, неотличимой от любой другой единицы, и, следовательно, может быть представлено числом одни. Однако, поскольку оно познаваемо и в других отношения, потребуется массив чисел для представления различных ситуаций, в которые оно может входить.

В соответствии с последовательностью категорий представление должно начинаться с целостности. Мы воспользуемся термином "точка" для обозначения целого безотносительно к бытию или функции. Первичный жест – акт представления – есть жест указания и "выделения точки"[3], который равносилен фиксации одного целого А как отличного от всех других целых не-А. Жест, фиксирующий точку как целое, закончен в себе. Он игнорирует все, кроме обозначаемой точки и, следовательно, не достигает категории полярности. Следовательно, точка не имеет ни силы, ни величины. Каждое целое, понимаемое только как целое, может быть представлено точкой.

Категория полярности может быть эксплицирована, только когда есть две независимые точки. Мы будем использовать термин "интервал" для обозначения этого уникального свойства, которое определяется двумя точками А и В безотносительно к какому-либо другому целому. Ввиду этого последнего условия интервал не имеет направления. В геометрии трехмерного пространства интервал – это длина и ничего более. Во временном измерении это не что иное как продолжительность. Детерминирующие условия вечности и гипарксиса также должны иметь свои интервалы, и там, где это должно быть специфицировано, мы пользуемся терминами "апокритический интервал" и "гипархческий интервал". Жест, обозначающий интервал, является жестом разделения и, следовательно, предполагает силу. Интервал между двумя геометрическими точками не содержит силу в физическом смысле и, тем не менее, он передает понятие полярности. Однако, это просто полярность без соотнесенности. Для обозначения интервала между двумя точками А и В, независимо от их природы, мы будем использовать символ /АВ/. Слово "интервал" берется в одном и том же смысле, имеет ли оно отношение к длинам или продолжительностям, которые мы можем измерять, или к апокризису и гипарксису, ускользающим от нашего наблюдения.

Чтобы обозначить отношение, мы вводим третий символ, а именно – вектор. Вектор не может быть определен в терминах только интервала; он имеет направление и величину, и они могут быть установлены только посредством отнесения, независимого от точек А и В, которыми задается векторный интервал. Жест, связывающий А и В, не имеет значения, если он не включает разделяющую их силу. Вектор, следовательно, - это представление акта преодоления сопротивления. Переход от А к В связывает А с В и В с А, но делает это таким образом, что различает эти два направления. Когда предполагается, А и В – это известные сущности, мы представляем соединяющий их вектор символом 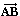. Когда мы хотим обозначить векторный жест без ссылки на две особые сущности, мы используем символ V. Несколько различных векторов обозначаются символами того же вида V, W, U и т.д.

Предположим, что для представления любой возможной оказии требуются N независимых числовых множеств. Тогда точка определяется как комбинация N чисел, взятых по одному из каждого множества.[4]

Необходимо также определить четвертый символ [N] – N-мерное многообразие – обозначающий многообразие, каждая точка которого единственным образом определена при помощи независимых чисел. Отдельная точка – это [0], линия - [1], поверхность - [2], и т.д. Говорят, что [N] имеет N измерений. Любые две точки А и В из [N] единственным образом определяют интервал, представляемый символом /АВ/. Могут существовать также векторы 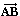, имеющие как величину, так и направление, но не обязательно уникальные, так как качества, переносимые от А к В, могут различаться. Векторы сами по себе не могут служить для представления таких многомерных переходов; но, как будет показано позже, может быть построена такая геометрия, в которой могут быть определены семейства векторов с необходимыми свойствами. Они будут называться пучками, и их применение к физическим проблемам является одним из принципиально новых математических методов, принимаемых в данной работе.

В дополнение к этим пяти первичным символам необходимые операции могут представляться при помощи обычных математических символов суммирования, дифференцирования и комбинации матриц и тензоров. Другим понятиям, таким как тождественность, конгруэнтность, равенство и неравенство могут быть присвоены их обычные значения, хотя, как это обнаружится позднее, некоторые из них окажутся подверженными относительности значения, сопровождающей все утверждения о бытии и существовании.

5.13.6.  ГЕОМЕТРИЯ

Геометрия – это наука, изучающая представление системы координат безотносительно к существованию. Представляющее многообразие должно обладать таким числом степеней свободы, каково количество выделенных независимых величин. Например, актуализация одномерна, последовательна и нетранзитивна. Следовательно, она может быть представлена посредством [1], где векторы различаются только по величине, а не по направлению, и, следовательно, неотличимы от интервалов. Потенциальность одномерна и транзитивна. Ее может представлять [1], где векторы можно различать при помощи неравенства "больше чем – меньше чем", присущего всем интервалам вечности. Гипарксис многомерен и не является ни последовательным, ни подлежащим различению потенциальностей. Хотя он рекуррентен и, следовательно, по существу, квантуется, он может быть представлен непрерывным многообразием размерности H. Время, вечность и гипарксис вместе составляют внутренние детерминирующие условия любого данного целого Р, и в объединении они дают [N], где значение N зависит от размерности гипарксиса, в настоящее время нам неизвестной.

Все внешние отношения А к не-А могут быть представлены числовым массивом, соответствующим нашему обычному представлению о пространстве. Нам известно из опыта, что пространство может быть представлено многообразием [3]. Однако оно не изотропно, то есть не все его направления эквивалентны. Например, для любого данного целого всегда существует уникальное направление, связывающее один момент актуализации с другим. "Мгновенное направление движения" является способом, которым мы испытываем это особое пространство-подобное направление любого и каждого целого А. Мы обозначим его символом Х, и числовое значение Х будет являться мерой влияния актуализации Р на другие целые.

Существует также направление результирующей всех сил, действующих на А вследствие его собственного вечностного потенциала. Оно, вообще говоря, не зависит от X и может быть представлено символом Y. Наконец, существует направление, в котором тело "способно быть собой". В простейшем случае это нейтральное направление, в котором нет ни движения, ни силы. В случае планет можно определить это третье направление как их  ось вращения. Оно будет обозначено символом Z.

Существуют, таким образом, три внешние направления, соответствующие трем внутренним детерминирующим условиям. Первые представляют собой условия внешнего для А мира, а последние – условия его внутреннего мира. В соответствии с этим анализом мы можем ожидать, что для представления А потребуется не менее шести числовых множеств, и, следовательно представляющее многообразие будет иметь шесть или больше измерений. Позже будет показано, что если задан характер внутренних детерминирующих условий и требование, что они должны быть полностью связаны с внешним миром А, то представляющее многообразие размерности шесть является необходимым и достаточным.

"Способность быть" данного целого А можно оценить только когда оно противопоставлено другим целым В, С, и т.д., с которыми оно может взаимодействовать. До тех пор, пока все его взаимодействия можно не принимать во внимание, целое можно рассматривать как стационарное в гипарксисе, и геометрия тогда сводится к пятимерной схеме времени, вечности и пространства.

5.13.7. ВЕЧНОСТЬ КАК ПЯТОЕ ИЗМЕРЕНИЕ

Геометрия, созданная Минковским для представления специальной теории относительности Эйнштейна, различает внутренние и внешние детерминирующие условия каждого целого, но ограничивает первые последовательностью во времени. Это дает многообразие [4]. Здесь необходимо представить тот факт, что внутренний мир должен соответствовать внешнему, и поэтому необходимо, чтобы в каждой точке контакта двух миров интервалы и векторы исчезали. Минковский выполнил это требование, рассматривая скорость света как универсальную константу, устанавливающую соотношение между время-подобными и пространство-подобными интервалами. В этом случае при построении представляющего многообразия, посредством которого можно сравнивать и соотносить внутренний и внешний миры любого целого, вполне пригодна индефинитная метрика. Мы расширим принадлежащий Минковскому метод построения однородного многообразия, в котором он использует конечную скорость света как фактор перехода, вводя соответствующий фактор для связывания апокритических интервалов с длинами. Тогда мы можем записать следующую метрику представляющего многообразия в дифференциальной форме:

ds² = dx² + dy² + dz² – c²dt² – λ²da²  (13.2)

Здесь ds зависит только от значений отдельно взятых координат. Если бы все члены правой части уравнения (13.2) были положительными, многообразие могло быть названо евклидовым. Для обозначения особого характера метрики мы будем называть ее "плоской, но индетерминированной" или псевдо-евклидовой. Если вычеркнуть члены формы dx dy, то многообразие будет римановым, которое использовал Эйнштейн  при создании общей теории относительности.

В этом уравнении продолжительности и апокритические интервалы рассматриваются как мнимые, а длины как действительные, так что космические интервалы могут быть положительными, нулевыми или отрицательными. Если ds² положительно, интервал называется пространство-подобным; если ds² отрицательно – времяподобным; если ds² равно нулю, мы будем называть его нуль-интервалом.

Если мы возьмем два вектора ОА и ОВ, так что А и В находятся во внешнем мире О, то, интегрируя равенство (13.2) – многообразие, будучи псевдо-евклидовым, позволяет это – мы  можем получить величину АВ, выраженную через компоненты ОА и ОВ. Из предыдущего следует, что хотя ОА и ОВ могут быть оба конечными векторами, при этом величина АВ может быть нулевой. В этом случае АВ называется нуль-вектором. Поскольку значение АВ является также мерой величины угла между векторами ОА и ОВ, этот угол может быть назван нуль-углом /null-angle/. Он отличается от нулевого угла /zero angle/ тем, что две стороны его не совпадают, но при этом не образуют угла. Такая ситуация не может возникнуть ни в полностью внутреннем, ни в полностью внешнем мире О. Она представляет отношение, связывающее два мира. Именно из-за этого свойства специальную геометрию  с индефинитной метрикой можно использовать для представления физических событий.

Важность этого свойства недостаточно учитывалась при развитии геометрии, пригодной для представления физических событий. Тем не менее, идея пятимерного представляющего многообразия не нова и, действительно, физическое значение многомерных геометрий уже широко признано.

Необходимость шестимерной геометрии можно осознать, если мы соотнесем ее с тремя свойствами сохранения, общими для гипономных ситуаций в целом. Первое из них – это постоянство скорости света в абсолютном вакууме, независимо от движения источника света. В этом случае, как показал Минковский, требуется четырехмерное представляющее многообразие. Второе – сохранение  энергии, и заряда, что требует пятимерной схемы для рассмотрения движений с ускорением. Третье – сохранение углового момента или спина, который не зависит от других свойств сохранения и требует шести измерений для своего представления[5].

5.13.8.ТРАЕКТОРИЯ СУЩЕСТВОВАНИЯ И КОСМОДЕЗИЧЕСКАЯ

Теперь мы введем и определим несколько характеристических свойств схемы представления. В той мере, в какой данное целое А существует в себе и для себя, не обмениваясь хилэ с другими целыми, о нем говорят, что оно существует консервативно. Его существование зависит единственно от его собственного потенциального паттерна в вечности и, следовательно, вечностный паттерн должен быть самотождественным для всех актуализаций, поскольку в самом А нет ничего, что могло бы изменить его собственный паттерн. Существование А в любой данный момент может, следовательно, быть единственным образом определено при помощи двух числовых множеств, одно из которых отмечает его состояние актуализации, а другое – его потенциальный уровень. Оба эти числа относятся к внутреннему миру А и, фактически, исчерпывают содержание этого мира. Следовательно, мы можем назвать многообразие [2], в котором могут быть представлены все консервативные внутренние состояния А, траекторией существования /existential tract/. Все векторы, принадлежащие траектории существования, время-подобны, и они ничего не могут сообщить нам о связях А с другими целыми, отличными от него самого.

Интервалы траектории существования представляют возможные переходы от одного состояния А к другому. И наоборот, любой интервал, находящийся вне траектории существования, должен представлять переход, запрещенный до тех пор, пока сама А не изменится.

Рассмотрим теперь точку Р представляющего многообразия, которая указывает актуальное состояние данного целого Р в момент времени t_o. При возможности взаимообмена между внутренним и внешним мирами Р возможны различные актуализации. Однако консервативная актуализация возможна только одна, а именно – единственная свободная от взаимодействия. Это консервативное отображение может быть продолжено на бесконечно малый интервал ds, представляющий актуализацию Р, от точки Р в момент t_o   до точки Р´ в момент  t_o+dt. Если во второй точке, Р´, Р опять актуализируется консервативно, то существует другой уникальный интервал, тождественный первому. У нас есть, таким образом, ряд интервалов, которые представляют все актуализации Р, начинающиеся в точке Р и удовлетворяющие условию, что в них не может быть взаимодействия с каким-либо другим целым. Это множество интервалов можно назвать невынужденной актуализацией Р. Для соответствующего ей представляющего многообразия [1] мы можем использовать специальный термин "космодезическая" /cosmodesic/.

Мы можем использовать понятие невынужденности таким же образом, как сделал Ньютон при определении "прямолинейного" пути. Единственное различие – и оно является наиболее важным – что  этот путь не лежит необходимо в том же пространственно-временном многообразии, что и путь наблюдателя О, который не связан с Р. В то время как в соответствии со специальной теорией относительности пути О и Р могут расходиться во времени, они остаются в одном и том же пространстве-времени,  то есть в "абсолютном мире" Минковского. В нашей схеме представления нет абсолютного мира пространства и времени, поскольку возможно любое число путей, на которых пространство-время может быть связано с вечностью. Путь Р можно назвать "внутренне и внешне" прямым, то есть на нем не изменяется ни форма актуализации Р, ни его отношение с другими целыми. Следовательно, может существовать одна и только одна космодезическая, проходящая через две точки, и космодезическая является "абсолютно" кратчайшим путем. Другими словами, космодезическая должна являться прямой в псевдо-евклидовом представляющем многообразии. Поскольку направление космодезической не может зависеть ни от чего, кроме самого Р, она должна всегда находиться в фиксированном отношении к траектории существования О и составлять с ней [3], у которого два измерения принадлежат внутреннему миру Р и одно – внешнему.

В той мере, в какой актуализация Р рассматривается как движение в пространстве и времени, космодезическую можно назвать "истинным путем", а движение – консервативным. Эта формула, однако, слишком ограничена, поскольку прямизна космодезической и единственность траектории существования не зависят только от актуализации. Тем не менее их истинный характер может быть виден только гипотетическому универсальному наблюдателю, способному наблюдать всю ситуацию вне времени и рассматривать время и вечность как эквивалентные однородные направления. По отношению  к восприятию, ассоциированному с каким-либо конечным целым О, актуализирующимся в пространстве и времени, наблюдаемое тело Р может казаться движущимся по кривой. Представляющее многообразие допускает эту возможность благодаря своей индефинитной метрике, позволяющей прямой иметь криволинейные проекции на внешний мир данного наблюдателя О.

Мы не можем оставить вопрос о представлении, не подчеркнув что только факты могут быть представлены обсуждаемым образом. Не может быть представления феноменов. Естественный порядок представлен в нашем опыте конкретно как воля, актуализирующаяся в функции посредством бытия. Это опыт феноменов; мы являемся их свидетелями и хотим их познать. Сведение феномена к факту и представление факта при помощи математического языка и геометрических конструкций предпринимается в поисках знания. Порядок, который мы таким образом открываем, совершенствуя наши наблюдательные приборы и средства представления, являются проекцией регулярностей, которые, как мы верим не зависят от стадий редукции, которые таковы:

Опыт                          Феномены

Феномены                             Факт

Факт                           Представление

Благодаря этой независимости, источник которой лежит в гомогенности и самосогласованности естественного порядка, знание, которое мы приобретаем, может вести к новым функциональным приспособлениям в наших отношениях с нашим миром. Это приспособление завершает цикл и служит верификации правильности избранного пути.

5.14.9.НЕЧУВСТВИТЕЛЬНОСТЬ К ВЕЧНОСТИ

Представляющее многообразие строится с целью дать нам возможность использования математического языка для выражения нашего субъективного и объективного опыта изучаемых событий. Это не представляло бы трудностей, если бы органы чувственного восприятия человека могли соответствовать жестам, которые выражают связь между потенциальными и актуальными состояниями. Поскольку, однако, чувственное восприятие чувствительно только к актуализациям, а не к потенциальностям, данные, которые оно нам доставляет, могут обеспечить только косвенную оценку вечностного аспекта наблюдаемого целого.

Апокритический интервал воспринимается только как переход из одного состояния сознания в другое, но не как обмен энергией. В результате он ускользает от любого возможного наблюдения посредством органов чувств. Человек-наблюдатель, который не может измерить апокритический интервал, склонен разделять свой мир таким образом, который не соответствует полной внутренней значимости событий. Его внешний мир является ему только как процесс актуализации во времени, а в своем внутреннем мире он может воспринимать и воспринимает потенциальность. Ограниченность человеческого чувственного восприятия может быть названа невосприимчивостью к вечности. Из-за нее человек, хотя и распознает трехмерность своего внешнего мира, но склонен рассматривать свой внутренний мир как одномерный. В результате все события проектируются в его внутренний мир, как если бы они составляли единственную актуализацию. Это случается даже тогда, когда само событие содержит апокритические перемещения, то есть переход опыта с одного уровня вечности на другой.

Простейшей иллюстрацией нечувствительности человека к вечности может являться тот факт, что мы не воспринимаем потенциальную энергию посредством органов чувств, и лишь выводим ее существование из закона сохранения энергии. Другим следствием невосприимчивости к вечности является то, что человек не может осознавать значимости нуль-векторов. Он  не может прямо производить измерения, необходимые для определения положения некоторого данного целого в космическом многообразии, которое представляло бы полностью его отношение к другим целым. Здесь следует подчеркнуть, что нечувствительность к вечности не присуща природе человека в силу порядка его бытия, но возникает лишь из-за нашей привычки ограничивать внимание чувственными впечатлениями и пренебрегать различениями сознания, постоянно возникающими в нашем внутреннем мире.

5.14.10. УНИВЕРСАЛЬНЫЙ НАБЛЮДАТЕЛЬ Q

Человек-наблюдатель не может установить для себя пятимерную систему координат как систему отнесения, так как все, что он делает, кажется ему ограниченным четырьмя измерениями его собственного чувственного опыта. Мы можем, однако, постулировать универсального наблюдателя, свободного от ограничений нечувствительности к вечности. Мы будем использовать символ Q для универсального наблюдателя и О для человека-наблюдателя, тогда как Р обозначает наблюдаемое тело. Значимость Q не ограничивается его способностью производить измерения на траектории существования, но в настоящий момент нам нет необходимости исследовать все значения, которые может нести этот символ.

Мы предполагаем, что Q выполняет действия того же типа, что и человек-наблюдатель, то есть он может создавать и использовать аппарат для измерения длин, углов, продолжительностей и масс. Он может, кроме того, при помощи аппарата такого рода, который мы не можем себе представить, измерять апокритические интервалы и исследовать траектории существования и космодезические тел. Он живет в пятимерном мире, с тем преимуществом перед О, что он свободно наблюдает перемещения в направлении вечности. Кроме этого Q актуализируется во времени как и О и записывает свои наблюдения в виде функций от времени как независимой переменной. Чтобы привести  свои наблюдения в форму, удобную для математического анализа, Q нуждается в построении собственной схемы представления.

Для того чтобы построить собственное представляющее многообразие, Q должен определить направления и проделать измерения, не будучи ограничен различием актуального и потенциального для данного состояния. Открыв постоянство скорости света, О способен провести прямое сравнение длин и продолжительностей. Универсальный наблюдатель Q может пойти дальше и проводить прямое сравнение длин, продолжительностей и апокризисов. Это дает ему возможность составить собственное метрическое уравнение в однородной форме, в котором все интервалы приводятся к общей мере. Таким образом, он способен сделать для пяти измерений то, что Минковский выполнил для пространства и времени. В то время как сознание О ограничено локальной системой, Q можно рассматривать как сознание, ассоциирующееся с общей системой масс во вселенной. Последняя должна иметь одну смыкающуюся актуализацию, которая определяет уникальное направление времени. Q также должен наблюдать уникальное направление вечности, а именно то, в исходной точке  которого вся вселенная находится в неактуализированном состоянии: оно может быть названо универсальным градиентом потенциала. Эти два фундаментальных космических направления всегда должны быть независимы и, следовательно, им могут соответствовать ортогональные оси в представляющем многообразии. Более того, Q, сознавая все потенциальности, присутствующие в каждой пространственной конфигурации, должен быть способен построить три измерения пространства, ортогональные его траектории существования. Другими словами, Q может непосредственно использовать космическое многообразие в качестве средства представления всех своих наблюдений оказий во времени и в вечности. Таким образом, Q способен составить уравнение для интервала, приведенного в (13.2), О не может выполнить необходимые наблюдения непосредственно, но он может вывести истинность (13.2) из комбинации собственных измерений и своих гипотез существования.